题目内容
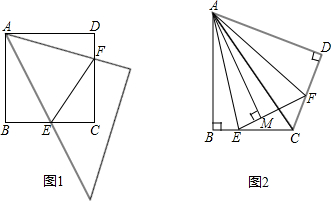
(2013•锦州)如图1,等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合,将此三角板绕点A旋转,使三角板中该锐角的两条边分别交正方形的两边BC,DC于点E,F,连接EF.
(1)猜想BE、EF、DF三条线段之间的数量关系,并证明你的猜想;
(2)在图1中,过点A作AM⊥EF于点M,请直接写出AM和AB的数量关系;
(3)如图2,将Rt△ABC沿斜边AC翻折得到Rt△ADC,E,F分别是BC,CD边上的点,∠EAF=
∠BAD,连接EF,过点A作AM⊥EF于点M,试猜想AM与AB之间的数量关系.并证明你的猜想.
(1)猜想BE、EF、DF三条线段之间的数量关系,并证明你的猜想;
(2)在图1中,过点A作AM⊥EF于点M,请直接写出AM和AB的数量关系;
(3)如图2,将Rt△ABC沿斜边AC翻折得到Rt△ADC,E,F分别是BC,CD边上的点,∠EAF=
| 1 | 2 |

分析:(1)延长CB到Q,使BQ=DF,连接AQ,根据四边形ABCD是正方形求出AD=AB,∠D=∠DAB=∠ABE=∠ABQ=90°,证△ADF≌△ABQ,推出AQ=AF,∠QAB=∠DAF,求出∠EAQ=∠F,证△EAQ≌△EAF,推出EF=BQ即可;
(2)根据△EAQ≌△EAF,EF=BQ得出
×BQ×AB=
×FE×AM,求出即可;
(3)延长CB到Q,使BQ=DF,连接AQ,根据折叠和已知得出AD=AB,∠D=∠ABE=90°,∠BAC=∠DAC=
∠BAD,证△ADF≌△ABQ,推出AQ=AF,∠QAB=∠DAF,求出∠EAQ=∠FAE,证△EAQ≌△EAF,推出EF=EQ即可.
(2)根据△EAQ≌△EAF,EF=BQ得出
| 1 |
| 2 |
| 1 |
| 2 |
(3)延长CB到Q,使BQ=DF,连接AQ,根据折叠和已知得出AD=AB,∠D=∠ABE=90°,∠BAC=∠DAC=
| 1 |
| 2 |
解答:(1)EF=BE+DF,
证明:如答图1,延长CB到Q,使BQ=DF,连接AQ,
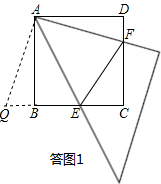
∵四边形ABCD是正方形,
∴AD=AB,∠D=∠DAB=∠ABE=∠ABQ=90°,
在△ADF和△ABQ中
,
∴△ADF≌△ABQ(SAS),
∴AQ=AF,∠QAB=∠DAF,
∵∠DAB=90°,∠FAE=45°,
∴∠DAF+∠BAE=45°,
∴∠BAE+∠BAQ=45°,
即∠EAQ=∠FAE,
在△EAQ和△EAF中
∴△EAQ≌△EAF,
∴EF=EQ=BE+BQ=BE+DF.
(2)解:AM=AB,
理由是:∵△EAQ≌△EAF,EF=BQ,
∴
×BQ×AB=
×FE×AM,
∴AM=AB.
(3)AM=AB,
证明:如答图2,延长CB到Q,使BQ=DF,连接AQ,
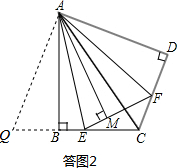
∵折叠后B和D重合,
∴AD=AB,∠D=∠ABE=90°,∠BAC=∠DAC=
∠BAD,
在△ADF和△ABQ中,
,
∴△ADF≌△ABQ(SAS),
∴AQ=AF,∠QAB=∠DAF,
∵∠FAE=
∠BAD,
∴∠DAF+∠BAE=∠BAE+∠BAQ=∠EAQ=
∠BAD,
即∠EAQ=∠FAE,
在△EAQ和△EAF中,
,
∴△EAQ≌△EAF(SAS),
∴EF=EQ,
∵△EAQ≌△EAF,EF=EQ,
∴
×EQ×AB=
×FE×AM,
∴AM=AB.
证明:如答图1,延长CB到Q,使BQ=DF,连接AQ,

∵四边形ABCD是正方形,
∴AD=AB,∠D=∠DAB=∠ABE=∠ABQ=90°,
在△ADF和△ABQ中
|
∴△ADF≌△ABQ(SAS),
∴AQ=AF,∠QAB=∠DAF,
∵∠DAB=90°,∠FAE=45°,
∴∠DAF+∠BAE=45°,
∴∠BAE+∠BAQ=45°,
即∠EAQ=∠FAE,
在△EAQ和△EAF中
|
∴△EAQ≌△EAF,
∴EF=EQ=BE+BQ=BE+DF.
(2)解:AM=AB,
理由是:∵△EAQ≌△EAF,EF=BQ,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴AM=AB.
(3)AM=AB,
证明:如答图2,延长CB到Q,使BQ=DF,连接AQ,

∵折叠后B和D重合,
∴AD=AB,∠D=∠ABE=90°,∠BAC=∠DAC=
| 1 |
| 2 |
在△ADF和△ABQ中,
|
∴△ADF≌△ABQ(SAS),
∴AQ=AF,∠QAB=∠DAF,
∵∠FAE=
| 1 |
| 2 |
∴∠DAF+∠BAE=∠BAE+∠BAQ=∠EAQ=
| 1 |
| 2 |
即∠EAQ=∠FAE,
在△EAQ和△EAF中,
|
∴△EAQ≌△EAF(SAS),
∴EF=EQ,
∵△EAQ≌△EAF,EF=EQ,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴AM=AB.
点评:本题考查了正方形的性质,全等三角形的性质和判定,折叠的性质的应用,主要考查学生综合运用定理进行推理的能力,题目比较典型,证明过程类似.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
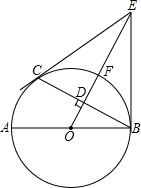 (2013•锦州)如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.
(2013•锦州)如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.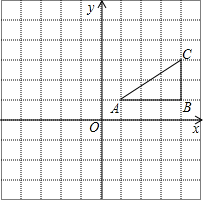 (2013•锦州)如图,方格纸中的每个小正方形边长都是1个长度单位,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,1),点B的坐标为(4,1).
(2013•锦州)如图,方格纸中的每个小正方形边长都是1个长度单位,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,1),点B的坐标为(4,1).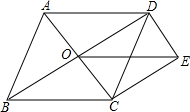 (2013•锦州)如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE.
(2013•锦州)如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE.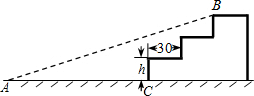 (2013•锦州)如图,某公司入口处有一斜坡AB,坡角为12°,AB的长为3m,施工队准备将斜坡修成三级台阶,台阶高度均为hcm,深度均为30cm,设台阶的起点为C.
(2013•锦州)如图,某公司入口处有一斜坡AB,坡角为12°,AB的长为3m,施工队准备将斜坡修成三级台阶,台阶高度均为hcm,深度均为30cm,设台阶的起点为C.