题目内容
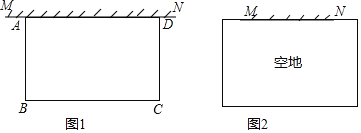
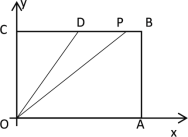
【题目】如图,在平面直角坐标系中,长方形![]() 的顶点
的顶点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() 是
是![]() 的中点,动点
的中点,动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度,沿着
个单位长度的速度,沿着![]() 运动,设点
运动,设点![]() 运动的时间为
运动的时间为![]() 秒(
秒(![]() ).
).
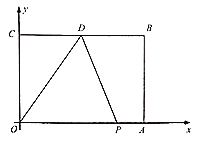
(1)点![]() 的坐标是______;
的坐标是______;
(2)当点![]() 在
在![]() 上运动时,点
上运动时,点![]() 的坐标是______(用
的坐标是______(用![]() 表示);
表示);
(3)求![]() 的面积
的面积![]() 与
与![]() 之间的函数表达式,并写出对应自变量
之间的函数表达式,并写出对应自变量![]() 的取值范围.
的取值范围.
【答案】(1)(3,4);(2)(6,t-6)(3)
【解析】
(1)根据长方形的性质和A、B的坐标,即可求出OA=BC=6,OC=AB=4,再根据中点的定义即可求出点D的坐标;
(2)画出图形,易知:点P的横坐标为6,然后根据路程=速度×时间,即可求出点P的运动路程,从而求出AP的长,即可得出点P的坐标;
(3)分别求出点P到达A、B、D三点所需时间,然后根据点P运动到OA、AB、BD分类讨论,并写出t对应的取值范围,然后画出图形,利用面积公式即可求出各种情况下![]() 与
与![]() 之间的函数表达式.
之间的函数表达式.
解:(1)∵长方形![]() 的顶点
的顶点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,
∴OA=BC=6,OC=AB=4,BA⊥x轴,BC⊥y轴
∵![]() 是
是![]() 的中点,
的中点,
∴CD=BD=![]() BC=3
BC=3
∴点D的坐标为(3,4)
故答案为:(3,4);
(2)当点![]() 在
在![]() 上运动时,如下图所示
上运动时,如下图所示

易知:点P的横坐标为6,
∵动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度,时间为t
个单位长度的速度,时间为t
∴点P运动的路程OA+AP=t
∴AP=t-6
∴点P的坐标为(6,t-6)
故答案为:(6,t-6);
(3)根据点P的速度可知:点P到达A点所需时间为OA÷1=6s
点P到达B点所需时间为(OA+AB)÷1=10s
点P到达D点所需时间为(OA+AB+BD)÷1=13s
①当点P在OA上运动时,此时![]() ,过点D作DE⊥x轴于E
,过点D作DE⊥x轴于E
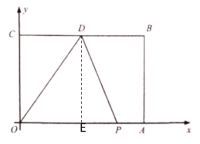
∴DE=4
∵动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度,
个单位长度的速度,
∴OP=t
∴![]() ;
;
②当点P在AB上运动时,此时![]() ,
,
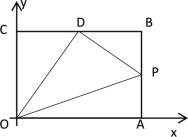
由(2)知AP=t-6
∴BP=AB-AP=10-t
∴![]()
=![]()
=![]()
=![]() ;
;
③当点P在BD上运动时,此时![]() ,
,
∵动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度,时间为t
个单位长度的速度,时间为t
∴点P运动的路程OA+AB+BP=t
∴BP=t-OA-AB=t-10
∴DP=BD-BP=13-t
![]()
=![]()
=![]()
综上所述:

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案