题目内容
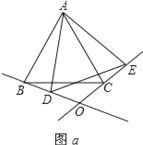
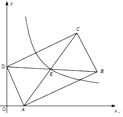
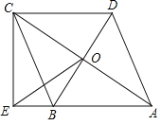
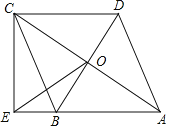
【题目】如图,在四边形ABCD中,对角线AC、BD交于点O,AB∥DC,AB=BC,BD平分∠ABC,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=2![]() ,BD=4,求OE的长.
,BD=4,求OE的长.
【答案】(1)见解析;(2)4
【解析】
(1)由平行线性质和角平分线性质易证明,BC=CD,因为AB∥CD且AB=BC,即可证明.
(2)直角三角形斜边的中线是斜边的一半,所以OE=OA=OC,菱形角平分线相互垂直平分,用勾股定理即可算出OC的长.
(1)∵AB∥CD,
∴∠ABD=∠CDB,
∵BD平分∠ABC,
∴∠ABD=∠CBD
∴∠CDB=∠CBD,
∴BC=CD,且AB=BC
∴CD=AB,且AB∥CD
∴四边形ABCD是平行四边形,且AB=BC
∴四边形ABCD是菱形;
(2)∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,BO=DO=2
∵AO=![]() =
=![]() =4
=4
∵CE⊥AB,AO=CO
∴EO=AO=CO=4.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目