Question

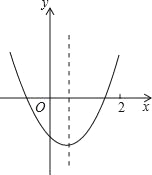
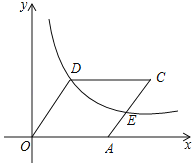
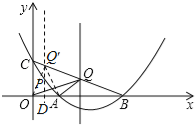
【题目】已知：如图，抛物线y=ax2+bx+2与x轴的交点是A（3，0）、B（6，0），与y轴的交点是C．

（1）求抛物线的函数表达式；

（2）设P（x，y）（0＜x＜6）是抛物线上的动点，过点P作PQ∥y轴交直线BC于点Q．

①当x取何值时，线段PQ的长度取得最大值，其最大值是多少？

②是否存在这样的点P，使△OAQ为直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）①x＝3，1；②P（3，0）或或．

【解析】

试题（1）已知了A，B的坐标，可用待定系数法求出函数的解析式．

（2）①QP其实就是一次函数与二次函数的差，二次函数的解析式在（1）中已经求出，而一次函数可根据B，C的坐标，用待定系数法求出．那么让一次函数的解析式减去二次函数的解析式，得出的新的函数就是关于PQ，x的函数关系式，那么可根据函数的性质求出PQ的最大值以及相对应的x的取值．

（3）分三种情况进行讨论：

当∠QOA=90°时，Q与C重合，显然不合题意．因此这种情况不成立；

当∠OAQ=90°时，P与A重合，因此P的坐标就是A的坐标；

当∠OQA=90°时，如果设QP与x轴的交点为D，那么根据射影定理可得出DQ2=ODDA．由此可得出关于x的方程即可求出x的值，然后将x代入二次函数式中即可得出P的坐标．

解：（1）∵抛物线过A（3，0），B（6，0），

∴，

解得：，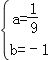

∴所求抛物线的函数表达式是y=x2﹣x+2．

（2）①∵当x=0时，y=2，

∴点C的坐标为（0，2）．

设直线BC的函数表达式是y=kx+h．

则有，

解得：．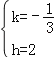

∴直线BC的函数表达式是y=﹣x+2．

∵0＜x＜6，点P、Q的横坐标相同，

∴PQ=yQ﹣yP=（﹣x+2）﹣（x2﹣x+2）

=﹣x2+x

=﹣（x﹣3）2+1

∴当x=3时，线段PQ的长度取得最大值．最大值是1．

②解：当∠OAQ′=90°时，点P与点A重合，

∴P（3，0）

当∠Q′OA=90°时，点P与点C重合，

∴x=0（不合题意）

当∠OQ′A=90°时，

设PQ′与x轴交于点D．

∵∠OQ′D+∠AOQ′=90°，∠Q′AD+∠AQ′D=90°，

∴∠OQ′D=∠Q′AD．

又∵∠ODQ′=∠Q′DA=90°，

∴△ODQ′∽△Q′DA．

∴，即DQ′2=ODDA．

∴（﹣x+2）2=x（3﹣x），

10x2﹣39x+36=0，

∴x1=，x2=，

∴y1=×（）2﹣+2=；

y2=×（）2﹣+2=；

∴P（，）或P（，）．

∴所求的点P的坐标是P（3，0）或P（，）或P（，）．