题目内容
已知:在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A、D、B三点,CB的延长线交⊙O于点E(如图1).在满足上述条件的情况下,当∠CAB的大小变化时,图形也随着改变(如图2),在这个变化过程中,有些线段总保持着相等的关系.
(1)观察上述图形,连接图2中已标明字母的某两点,得到一条新线段
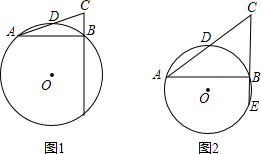 与线段CE相等,请说明理由;
与线段CE相等,请说明理由;(2)在图2中,过点E作⊙O的切线,交AC的延长线于点F.
①若CF=CD,求sin∠CAB的值;
②若
| CF | CD |
分析:(1)连接AE,由图不难看出OD是三角形ABC的中线,那么OD=
CE,又因为OD是半径,AE是直径,因此AE=CE;
(2)若CD=CF,那么AD=CD=CF,由图不难得出Rt△ADE∽Rt△EDF,那么就可用AD,DF表示出DE,然后根据直角三角形CDE中,CE2=CD2+DE2,这样就能表示出CE了,那么∠CED的正弦函数也就求出来了,∠CAB的正弦值也就有了.
| 1 |
| 2 |
(2)若CD=CF,那么AD=CD=CF,由图不难得出Rt△ADE∽Rt△EDF,那么就可用AD,DF表示出DE,然后根据直角三角形CDE中,CE2=CD2+DE2,这样就能表示出CE了,那么∠CED的正弦函数也就求出来了,∠CAB的正弦值也就有了.
解答:解:(1)连接AE,
求证:AE=CE.
证明:如图,连接OD,
∵∠ABC=90°,CB的延长线交⊙O于点E,
∴∠ABE=90°
∴AE是⊙O的直径,
∵D是AC的中点,O是AE的中点,
∴OD=
CE
∵OD=
AE
∴AE=CE.
(2)①根据题意画出图形,如图,连接DE,
∵AE是⊙O的直径,EF是⊙O的切线,
∴∠ADE=∠AEF=90°,
∴Rt△ADE∽Rt△EDF,
∴
=
.
设AD=k(k>0),则DF=2k,
∴
=
,
∴DE=
k.
在Rt△CDE中,
∵CE2=CD2+DE2=k2+(
k)2=3k2,
∴CE=
k,
∵∠ABC=∠EDC=90°,∠ACB=∠DCE,
∴∠CAB=∠DEC,
sin∠CAB=sin∠DEC=
=
.
②sin∠CAB=
(n>0).
求证:AE=CE.

证明:如图,连接OD,
∵∠ABC=90°,CB的延长线交⊙O于点E,
∴∠ABE=90°
∴AE是⊙O的直径,
∵D是AC的中点,O是AE的中点,
∴OD=
| 1 |
| 2 |
∵OD=
| 1 |
| 2 |
∴AE=CE.
(2)①根据题意画出图形,如图,连接DE,
∵AE是⊙O的直径,EF是⊙O的切线,

∴∠ADE=∠AEF=90°,
∴Rt△ADE∽Rt△EDF,
∴
| AD |
| DE |
| DE |
| DF |
设AD=k(k>0),则DF=2k,
∴
| k |
| DE |
| DE |
| 2k |
∴DE=
| 2 |
在Rt△CDE中,
∵CE2=CD2+DE2=k2+(
| 2 |
∴CE=
| 3 |
∵∠ABC=∠EDC=90°,∠ACB=∠DCE,
∴∠CAB=∠DEC,
sin∠CAB=sin∠DEC=
| CD |
| CE |
| ||
| 3 |
②sin∠CAB=
| ||
| n+2 |
点评:本题综合考查了切线的性质,相似三角形,解直角三角形等知识点的运用.此题是一个大综合题,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
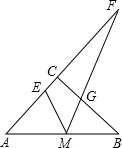 如图,已知:在Rt△ABC中,∠ACB=90°,AC=BC=4,M是边AB的中点,E、G分别是边AC、BC上的一点,∠EMG=45°,AC与MG的延长线相交于点F.
如图,已知:在Rt△ABC中,∠ACB=90°,AC=BC=4,M是边AB的中点,E、G分别是边AC、BC上的一点,∠EMG=45°,AC与MG的延长线相交于点F.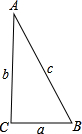 已知:在Rt△ABC中,∠C=90°,∠A=30°,b=
已知:在Rt△ABC中,∠C=90°,∠A=30°,b=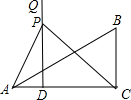 重合),过D作DQ⊥AC(DQ与AB在AC的同侧);点P从D点出发,在射线DQ上运动,连接PA、PC.
重合),过D作DQ⊥AC(DQ与AB在AC的同侧);点P从D点出发,在射线DQ上运动,连接PA、PC.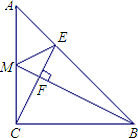 已知:在Rt△ABC中,∠C=90°,AC=BC,M是AC的中点,连接BM,CF⊥MB,F是垂足,延长CF交AB于点E.求证:∠AME=∠CMB.
已知:在Rt△ABC中,∠C=90°,AC=BC,M是AC的中点,连接BM,CF⊥MB,F是垂足,延长CF交AB于点E.求证:∠AME=∠CMB. 已知:在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.
已知:在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.