Question

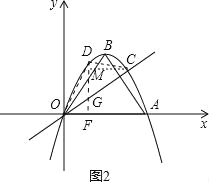
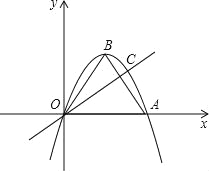
【题目】如图，在平面直角坐标系中，点O是原点，点A的坐标为（4，0），以OA为一边，在第一象限作等边△OAB

（1）求点B的坐标；

（2）求经过O、A、B三点的抛物线的解析式；

（3）直线y=x与（2）中的抛物线在第一象限相交于点C，求点C的坐标；

（4）在（3）中，直线OC上方的抛物线上，是否存在一点D，使得△OCD的面积最大？如果存在，求出点D的坐标和面积的最大值；如果不存在，请说明理由．

Answer 1

【答案】（1）点B的坐标为（2，2）；

（2）抛物线的解析式为y=﹣（x﹣2）2+2；

（3）点C的坐标为（3，）；

（4）△OCD的最大面积为，此时点D的坐标为（，）．

【解析】

试题分析：（1）利用点A的坐标为（4，0），△OAB是等边三角形，作高后利用勾股定理可以求出；

（2）题利用顶点式可以求出解析式；

（3）由直线y=x与抛物线相交，用x表示出点C的坐标，即可求出；

（4）假设存在这样一个点，用x表示出点D的坐标，即可求出．

试题解析：（1）如图1，过点B作BE⊥x轴于点E，∵△OAB是等边三角形，

∴OE=2，BE=2，∴点B的坐标为（2，2）；

（2）根据抛物线的对称性可知，点B（2，2）是抛物线的顶点，

设抛物线的解析式为y=a（x﹣2）2+2，

当x=0时，y=0，

∴0=a（0﹣2）2+2，∴a=﹣，

∴抛物线的解析式为y=﹣（x﹣2）2+2，

即：y=﹣x2+2x；

（3）设点C的横坐标为x，则纵坐标为x，

即点C的坐标为（x， x）代入抛物线的解析式得： x=﹣x2+2x，

解得：x=0或x=3，∵点C在第一象限，∴x=3，

∴点C的坐标为（3，）；

（4）存在．

设点D的坐标为（x，﹣ x2+2x），△OCD的面积为S，

如图2，过点D作DF⊥x轴于点F，交OC于点G，

则点G的坐标为（x， x），

作CM⊥DF于点M，

则OF+CM=3，DG=﹣x2+2x﹣x=﹣x2+x，

∴S=S△OCD=S△DGO+S△DGC=DGOF+DGCM=DG（OF+CM）=DG×3

=（﹣x2+x）×3，

∴S=﹣x2+x=﹣（x﹣）2+，

∴△OCD的最大面积为，此时点D的坐标为（，）．