题目内容
 【题目】如图,AD为△ABC的中线,BE为三角形ABD中线,
【题目】如图,AD为△ABC的中线,BE为三角形ABD中线,
(1)∠ABE=15°,∠BAD=35°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为60,BD=5,则点E到BC边的距离为多少?

【答案】(1)50°;(2)答案见解析;(3)6.
【解析】
试题分析:(1)根据∠BED是△ABE的一个外角得出答案;(2)根据高线的作法得出答案;(3)根据AD为△ABC的中线,BE为三角形ABD中线得出△BED的面积,然后根据等面积法求出EF的长度,从而得出点E到BC边的距离.
试题解析:(1)∵∠BED是△ABE的一个外角, ∴∠BED=∠ABE+∠BAD=15°+35°=50°.
(2)如图所示,EF即是△BED中BD边上的高.
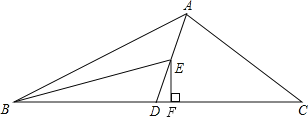
(3)∵AD为△ABC的中线,BE为三角形ABD中线, ∴S△BED=![]() S△ABC=
S△ABC=![]() ×60=15; ∵BD=5,
×60=15; ∵BD=5,
∴EF=2S△BED÷BD=2×15÷5=6, 即点E到BC边的距离为6.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目