题目内容
【题目】在平面直角坐标系中,直线AB分别交x轴,y轴于A(a,0),B(0,b),且满足a2+b2+4a﹣8b+20=0.

(1)求a,b的值;
(2)点P在直线AB的右侧;且∠APB=45°,
①若点P在x轴上(图1),则点P的坐标为 ;
②若△ABP为直角三角形,求P点的坐标.
【答案】(1)a=﹣2,b=4;(2)①(4,0);②P点坐标为(4,2),(2,﹣2).
【解析】
(1)利用非负数的性质解决问题即可.
(2)①根据等腰直角三角形的性质即可解决问题.
②分两种情形:如图2中,若∠ABP=90°,过点P作PC⊥OB,垂足为C.如图3中,若∠BAP=90°,过点P作PD⊥OA,垂足为D.分别利用全等三角形的性质解决问题即可.
(1)∵a2+4a+4+b2﹣8b+16=0
∴(a+2)2+(b﹣4)2=0
∴a=﹣2,b=4.
(2)①如图1中,
∵∠APB=45°,∠POB=90°,
∴OP=OB=4,
∴P(4,0).
故答案为(4,0).
②∵a=﹣2,b=4
∴OA=2OB=4
又∵△ABP为直角三角形,∠APB=45°
∴只有两种情况,∠ABP=90°或∠BAP=90°
①如图2中,若∠ABP=90°,过点P作PC⊥OB,垂足为C.
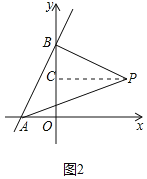
∴∠PCB=∠BOA=90°,
又∵∠APB=45°,
∴∠BAP=∠APB=45°,
∴BA=BP,
又∵∠ABO+∠OBP=∠OBP+∠BPC=90°,
∴∠ABO=∠BPC,
∴△ABO≌△BPC(AAS),
∴PC=OB=4,BC=OA=2,
∴OC=OB﹣BC=4﹣2=2,
∴P(4,2).
②如图3中,若∠BAP=90°,过点P作PD⊥OA,垂足为D.
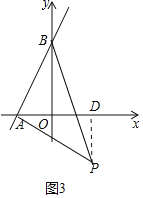
∴∠PDA=∠AOB=90°,
又∵∠APB=45°,
∴∠ABP=∠APB=45°,
∴AP=AB,
又∵∠BAD+∠DAP=90°,
∠DPA+∠DAP=90°,
∴∠BAD=∠DPA,
∴△BAO≌△APP(AAS),
∴PD=OA=2,AD=OB=4,
∴OD=AD﹣0A=4﹣2=2,
∴P(2,﹣2).
综上述,P点坐标为(4,2),(2,﹣2).

 名师点拨卷系列答案
名师点拨卷系列答案