题目内容
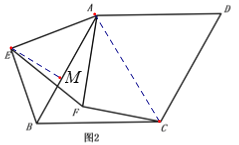
【题目】已知如图1菱形ABCD,∠ABC=60o,边长为3,在菱形内作等边三角形△AEF,边长为![]() ,点E,点F,分别在AB,AC上,以A为旋转中心将△AEF顺时针转动,旋转角为α,如图2.
,点E,点F,分别在AB,AC上,以A为旋转中心将△AEF顺时针转动,旋转角为α,如图2.
(1)在图2中证明BE=CF;
(2)若∠BAE=45o,求CF的长度;
(3)当CF=![]() 时,直接写出旋转角α的度数。
时,直接写出旋转角α的度数。


【答案】(1)证明见解析;
(2)CF的长度为![]() ;
;
(3)旋转角α的度数为90o或270o。
【解析】试题分析:
试题解析:(1)连接AC,由菱形ABCD,∠ABC=60o得:△ABC是等边三角形,∴AB=AC,∠BAC=60°,∵△AEF为等边三角形,∴AE=AF,∠EAF=60°,∴∠EAB=∠FAC,∴△AEB≌△AFC(SAS),∴BE=CF;
(2)过E点作EM垂直AB垂足为M,则∠AME=90°,∵∠BAE=45°,∴AM=EM,∵AM2+EM2=AE2,AE=2![]() ,∴AM=EM=2,∵AB=3,∴BM=1,∴BE=
,∴AM=EM=2,∵AB=3,∴BM=1,∴BE=![]() ,∴CF=BE=
,∴CF=BE=![]() ;
;
(3)90o或270o

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】(6分)小聪是个数学爱好者,他发现从1开始,连续几个奇数相加,和的变化规律如右表所示:
加数个数 | 连续奇数的和S |
1 | 1= |
2 | 1+3=22 |
3 | 1+3+5=32 |
4 | 1+3+5+7=42 |
5 | 1+3+5+7+9=52 |
n | … |
(1)如果n=7,则S的值为 ;
(2)求1+3+5+7+…+199的值;
(3)求13+15+17+…+79的值.