��Ŀ����
����Ŀ��ij�ľ����۵����������г�ѡ��A��B�����ľߣ�������A��Ϊ12Ԫ/����B��Ϊ8Ԫ/�������õ�����A��B�����ľߵ���������y�����������ۼ�x��Ԫ/��������һ�κ�����ϵ������ͼ��
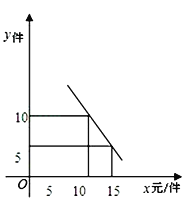
��1����y��x�ĺ�����ϵʽ��
��2���õ�ƻ����ѡ��A��B�����ľߵ�������100���������ʽ���1000Ԫ����ϣ��ȫ���������������296Ԫ������A���ľ�ÿ���ɻ���4Ԫ��B���ľ�ÿ���ɻ���2Ԫ���㣬��õ�������ļ��ֽ���������
��3����A���ľߵ����ۼ۱�B���ľߵ����ۼ۸�2Ԫ/�����������ľ�ÿ�����������W��Ԫ����A���ľ����ۼ�x��Ԫ/����֮��ĺ�����ϵʽ����˵��A��B�����ľ����ۼ۷ֱ�Ϊ����ʱ��ÿ�����۵��������
���𰸡���1��y=-x+20����2�������ֽ�����������A��48����B��52������A��49����B��51������A��50����B��50������3����A���ľ����ۼ�Ϊ16Ԫ/����B���ľ����ۼ�Ϊ14Ԫ/��ʱ��ÿ�����۵��������
�������������������1����y=kx+b���ѵ㣨10,10������15,5�����룬Ȼ��ⷽ���鼴�ɣ���2������ι���A���ľ�a����Ȼ����ݹ�ϵ�������ʽ���1000Ԫ����ϣ��ȫ���������������296Ԫ���в���ʽ���ȷ��x��ȡֵ��Χ��Ȼ��ȷ�������⼴�ɣ���3�����w��z�ĺ�����ϵʽ��Ȼ����ݶ��κ���������������������ֵ���ɣ�
����������⣺��1����y=kx+b����![]() ��
��
���![]() ��
��
��y��x�ĺ�����ϵʽΪy=-x+20��
��y=4������ʱ��x=16��Ԫ������A���ľ�ÿ������16-12=4��Ԫ����
����ι���A���ľ�a������B���ľߣ�100-a������
��![]() �����48��a��50��
�����48��a��50��
��a��������a=48��49��50��
������������ֽ�����������A��48����B��52������A��49����B��51������A��50����B��50����
��3���������W=��x-12����-x+20��+��x-2-8��[-��x-2��+20]��
��W=-2x2+64x-460=-2��x-16��2+52��
����A���ľ����ۼ�Ϊ16Ԫ/����B���ľ����ۼ�Ϊ14Ԫ/��ʱ��ÿ�����۵��������