题目内容
已知有理数a,b,c满足①5(x-y+3)2+2|m-2|=0;②n3a2-yb5+z是一个三次单项式且系数为-1:(1)求m,n的值; (2)求代数式(x-y)m+1+(y-z)1-n+(z-x)5的值.
分析:根据已知和所求问题,首先由5(x-y+3)2+2|m-2|=0,得出(x-y+3)2=0,
=0,求出x-y和m.再由n3a2-yb5+z是一个三次单项式且系数为-1,得出n3=-1和2-y+5+z=3,求出y-z和n.最后,由x-y和y-z求出x-z.
|
解答:解:(1)∵5(x-y+3)2+2|m-2|=0,(x-y+3)2≥0,
≥0,及n3a2-yb5+z是一个三次单项式且系数为-1.
∴得:
∴
(2)由(1)得
∴x-z=x-y+y-z=1
∴z-x=-1
∴原式=(-3)3+42+(-1)5=-12
|
∴得:
|
|
(2)由(1)得
|
∴x-z=x-y+y-z=1
∴z-x=-1
∴原式=(-3)3+42+(-1)5=-12
点评:此题考查了学生整体代入法求代数式的值、非负数的性质、单项式等的理解与掌握.关键是根据已知有关性质列等式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


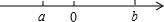 已知有理数a,b所对应的点在数轴上如图所示,化简|b-a|得( )
已知有理数a,b所对应的点在数轴上如图所示,化简|b-a|得( )