题目内容
如图,已知直线y=x+4与x轴、y轴分别相交于点A、B,点M是线段AB(中点除外)上的动点,以点M为圆心,OM的长为半径作圆,与x轴、y轴分别相交于点C、D.
(1)设点M的横坐标为a,则点C的坐标为 ,点D的坐标为 (用含有a的代数式表示);
(2)求证:AC=BD;
(3)若过点D作直线AB的垂线,垂足为E.
①求证: AB=2ME;
②是否存在点M,使得AM=BE?若存在,求出点M的坐标;若不存在,请说明理由.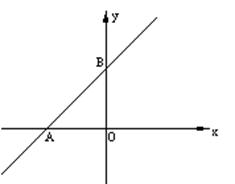
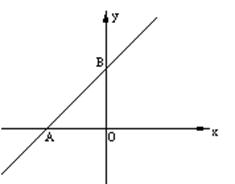
(1)设点M的横坐标为a,则点C的坐标为 ,点D的坐标为 (用含有a的代数式表示);
(2)求证:AC=BD;
(3)若过点D作直线AB的垂线,垂足为E.
①求证: AB=2ME;
②是否存在点M,使得AM=BE?若存在,求出点M的坐标;若不存在,请说明理由.


⑴C(2a,0),D(0,2a+8)
⑵方法一:由题意得:A(-4,0),B(0,4)
-4<a<0,且a≠2,
① 当2a+8<4,即-4<a<-2时
AC=-4-2a,BD=4-(2a+8)=-4-2a
∴AC=BD
② 当2a+8>4,即-2<a<0时
同理可证:AC=BD
综上:AC=BD
方法二:①当点D在B、O之间时,
连CD,∵∠COD=90°
∴圆心M在CD上,
过点D作DF∥AB,
∵点M为CD中点,
∴MA为△CDF中位线,
∴AC=AF,
又DF∥AB,
∴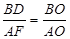 ,
,
而BO=AO
∴AF=BD
∴AC=BD
②点D在点B上方时,同理可证:AC=BD
综上:AC=BD
⑶方法一
①A(-4,0),B(0,4),D(0,2a+8),M(a,a+4),△BDE、△ABO均为等腰直角三角形,
E的纵坐标为a+6,∴ME= (yE-yM)=
(yE-yM)= =2
=2
AB=4
∴AB=2ME
②AM= ( yM-yA)=
( yM-yA)= (a+4),BE=
(a+4),BE= |yE-yB|=
|yE-yB|= |a+2|,
|a+2|,
∵AM=BE
又-4<a<0,且a≠2,
10 当-4<a<-2时
 (a+4)= -
(a+4)= - (a+2)
(a+2)
∴a=-3
M(-3,1)
20 当-2<a<0时
 (a+4)=
(a+4)=  (a+2)
(a+2)
∴a不存在
方法二:
①当点D在B、O之间时,作MP⊥x轴于点P、MQ⊥y轴于点Q,取AB中点N,
在Rt△MNO与Rt△DEM中,MO=MD
∠MON=450-∠MOP
∠EMD=450-∠DMQ=450-∠OMQ=450-∠MOP
∴∠MON=∠EMD
∴Rt△MNO≌Rt△DEM
∴MN=ED=EB
∴AB=2NB=2(NE+EB)=2(NE+MN)=2ME
当点D在点B上方时,同理可证
②当点D在B、O之间时,
由①得MN=EB,
∴AM=NE
若AM=BE,则AM=MN=NE=EB=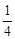 AB=
AB=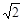
∴M(-3,1)
点D在点B上方时,不存在。
⑵方法一:由题意得:A(-4,0),B(0,4)
-4<a<0,且a≠2,
① 当2a+8<4,即-4<a<-2时
AC=-4-2a,BD=4-(2a+8)=-4-2a
∴AC=BD
② 当2a+8>4,即-2<a<0时
同理可证:AC=BD
综上:AC=BD
方法二:①当点D在B、O之间时,
连CD,∵∠COD=90°
∴圆心M在CD上,
过点D作DF∥AB,
∵点M为CD中点,
∴MA为△CDF中位线,
∴AC=AF,
又DF∥AB,
∴
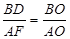 ,
,而BO=AO
∴AF=BD
∴AC=BD
②点D在点B上方时,同理可证:AC=BD
综上:AC=BD
⑶方法一
①A(-4,0),B(0,4),D(0,2a+8),M(a,a+4),△BDE、△ABO均为等腰直角三角形,
E的纵坐标为a+6,∴ME=
 (yE-yM)=
(yE-yM)= =2
=2
AB=4

∴AB=2ME
②AM=
 ( yM-yA)=
( yM-yA)= (a+4),BE=
(a+4),BE= |yE-yB|=
|yE-yB|= |a+2|,
|a+2|,∵AM=BE
又-4<a<0,且a≠2,
10 当-4<a<-2时
 (a+4)= -
(a+4)= - (a+2)
(a+2)∴a=-3
M(-3,1)
20 当-2<a<0时
 (a+4)=
(a+4)=  (a+2)
(a+2)∴a不存在
方法二:
①当点D在B、O之间时,作MP⊥x轴于点P、MQ⊥y轴于点Q,取AB中点N,
在Rt△MNO与Rt△DEM中,MO=MD
∠MON=450-∠MOP
∠EMD=450-∠DMQ=450-∠OMQ=450-∠MOP
∴∠MON=∠EMD
∴Rt△MNO≌Rt△DEM
∴MN=ED=EB
∴AB=2NB=2(NE+EB)=2(NE+MN)=2ME
当点D在点B上方时,同理可证
②当点D在B、O之间时,
由①得MN=EB,
∴AM=NE
若AM=BE,则AM=MN=NE=EB=
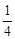 AB=
AB=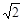
∴M(-3,1)
点D在点B上方时,不存在。
(1)直接利用垂径定理可知C(2a,0),D(0,2a+8);
(2)本题可用直角坐标系中两点间的距离公式分别求算出AC=-4-2a,BD=4-(2a+8)=-4-2a,所以AC=BD;
(3)①根据A(-4,0),B(0,4),D(0,2a+8),M(a,a+4),可知△BDE、△ABO均为等腰直角三角形,E的纵坐标为a+6,可求得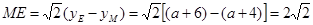 ,
,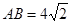 ,所以AB=2ME;
,所以AB=2ME;
②AM= (
( 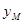 -
- )=
)= (a+4),BE=
(a+4),BE= |
|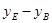 |=
|= |a+2|,AM=BE,结合条件-4<a<0,且a≠2,a=-3,可知M(-3,1);当-2<a<0时,a不存在。
|a+2|,AM=BE,结合条件-4<a<0,且a≠2,a=-3,可知M(-3,1);当-2<a<0时,a不存在。
(2)本题可用直角坐标系中两点间的距离公式分别求算出AC=-4-2a,BD=4-(2a+8)=-4-2a,所以AC=BD;
(3)①根据A(-4,0),B(0,4),D(0,2a+8),M(a,a+4),可知△BDE、△ABO均为等腰直角三角形,E的纵坐标为a+6,可求得
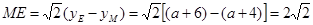 ,
,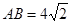 ,所以AB=2ME;
,所以AB=2ME;②AM=
 (
( 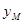 -
- )=
)= (a+4),BE=
(a+4),BE= |
|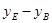 |=
|= |a+2|,AM=BE,结合条件-4<a<0,且a≠2,a=-3,可知M(-3,1);当-2<a<0时,a不存在。
|a+2|,AM=BE,结合条件-4<a<0,且a≠2,a=-3,可知M(-3,1);当-2<a<0时,a不存在。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 ,
, )
) ,
, )
)
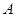 点坐标为(0,2),
点坐标为(0,2),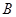 点坐标为(-2,0);
点坐标为(-2,0);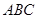 为等腰直角三角形,请画出所有符合条件的点
为等腰直角三角形,请画出所有符合条件的点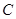 ,并直接写出相应的
,并直接写出相应的
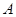 在
在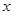 轴上,点
轴上,点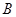 的坐标为(4,2),若四边形
的坐标为(4,2),若四边形 为菱形,则点
为菱形,则点 的坐标为 .
的坐标为 .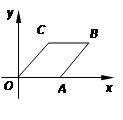
 的图象上,前面的四种描述正确的是【 】
的图象上,前面的四种描述正确的是【 】