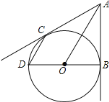
题目内容
【题目】如图，在菱形
中，
，点
、
分别是
、
上任意的点（不与端点重合），且
，连接
与
相交于点
，连接
与
相交于点
．给出如下几个结论：①
；②
；③与一定不垂直；④
的大小为定值．其中正确的结论有________．
【答案】①④
【解析】
①先证明△ABD为等边三角形，根据“SAS”证明△AED≌△DFB；
②证明∠BGE=60°=∠BCD，从而得点B、C、D、G四点共圆，因此∠BGC=∠DGC=60°，过点C作CM⊥GB于M，CN⊥GD于N．证明△CBM≌△CDN，所以S四边形BCDG=S四边形CMGN，易求后者的面积；
③过点F作FP∥AE于P点，根据题意有FP：AE=DF：DA=1：3，则FP：BE=1：6=FG：BG，即BG=6GF；因为点E、F分别是AB、AD上任意的点（不与端点重合），且AE=DF，当点E，F分别是AB，AD中点时，CG⊥BD；
④∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°．
①∵ABCD为菱形，∴AB=AD，
∵AB=BD，∴△ABD为等边三角形，
∴∠A=∠BDF=60°，
又∵AE=DF，AD=BD，
∴△AED≌△DFB，故本选项正确；
②∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD，
即∠BGD+∠BCD=180°，
∴点B、C、D、G四点共圆，
∴∠BGC=∠BDC=60°，∠DGC=∠DBC=60°，
∴∠BGC=∠DGC=60°，
过点C作CM⊥GB于M，CN⊥GD于N（如图1），
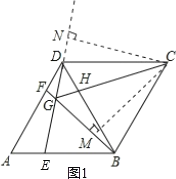
则△CBM≌△CDN（AAS），
∴S四边形BCDG=S四边形CMGN，
S四边形CMGN=2S△CMG，
∵∠CGM=60°，
∴
∴S四边形CMGN=2S△CMG
故本选项错误；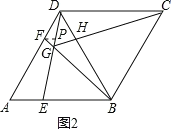
③当点E，F分别是AB，AD中点时（如图3），
由（1）知，△ABD，△BDC为等边三角形，
∵点E，F分别是AB，AD中点，
∴∠BDE=∠DBG=30°，
∴DG=BG，
在△GDC与△BGC中，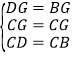
，
∴△GDC≌△BGC，
∴∠DCG=∠BCG，
∴CH⊥BD，即CG⊥BD，故本选项错误；
④∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°，为定值，
故本选项正确；
综上所述，正确的结论有①④，
故答案为：①④．
