题目内容
四边形ABCD中，∠A=∠BCD=90°，BC=CD，E是AD延长线上一点，若DE=AB=4cm，CE=3cm，则AD的长是________cm．
3
-4
分析：连接AC，那么可证得△ABC、△EDC全等，进而可得到△ACE是等腰直角三角形，在等腰Rt△ACE中，已知直角边CE的长，即可求得斜边AE的值，从而由AD=AE-DE得解．
解答：
解：如图；连接AC；
由于∠BAD=∠BCD=90°，那么∠B、∠ADC互补，
所以∠B=∠EDC；
又BA=DE，BC=CD，
∴△ABC≌△EDC，
∴AC=CE，∠BCA=∠DCE，即∠BCD=∠ACE=90°，
∴△ACE是等腰直角三角形；
已知CE=3cm，则AE=3cm，AD=AE-DE=（3-4）cm．
点评：此题主要考查的是全等三角形的判定和性质，准确作出辅助线，构造出全等三角形是解决问题的关键．
-4分析：连接AC，那么可证得△ABC、△EDC全等，进而可得到△ACE是等腰直角三角形，在等腰Rt△ACE中，已知直角边CE的长，即可求得斜边AE的值，从而由AD=AE-DE得解．
解答：
解：如图；连接AC；由于∠BAD=∠BCD=90°，那么∠B、∠ADC互补，
所以∠B=∠EDC；
又BA=DE，BC=CD，
∴△ABC≌△EDC，
∴AC=CE，∠BCA=∠DCE，即∠BCD=∠ACE=90°，
∴△ACE是等腰直角三角形；
已知CE=3cm，则AE=3
cm，AD=AE-DE=（3-4）cm．点评：此题主要考查的是全等三角形的判定和性质，准确作出辅助线，构造出全等三角形是解决问题的关键．
练习册系列答案
相关题目
23、如图，四边形ABCD中，对角线AC、BD相交于点E．已知：DA=DC，E为AC中点．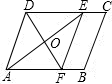
如图所示，在平行四边形ABCD中，AE是∠DAB的平分线，EF∥AD交AB于点F，若AB=9，CE=4，AE=8，则DF等于（ ）
17、如图，在平行四边形ABCD中，对角线AC、BD相交于点O，过点O的直线EF分别交AB、CD于E、F．请写出图中三对全等的三角形：
7、如图，在四边形ABCD中，AD=CB，∠ACB=∠CAD．求证：AB=CD．