题目内容
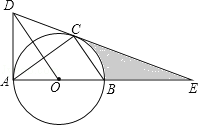
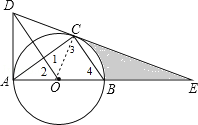
【题目】如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AE=6,CE=2![]() ,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
【答案】(1)、证明过程见解析;(2)、![]() .
.
【解析】
试题分析:(1)、连结OC,根据切线得出∠BAD=90°,然后得出△OCD和△OAD全等,从而得出∠OCD=∠OAD=90°,得出切线;(2)、设半径为r,则OE=AE﹣OA=6﹣r,OC=r,根据Rt△OCE的勾股定理求出r的值,然后根据△COE的面积减去扇形BOC的面积得出答案.
试题解析:(1)、连结OC,如图, ∵AD为⊙O的切线,∴AD⊥AB,∴∠BAD=90°,
∵OD∥BC,∴∠1=∠3,∠2=∠4, ∵OB=OC,∴∠3=∠4,∴∠1=∠2,
在△OCD和△OAD中,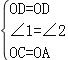 ,∴△AOD≌△COD(SAS); ∴∠OCD=∠OAD=90°,
,∴△AOD≌△COD(SAS); ∴∠OCD=∠OAD=90°,
∴OC⊥DE,∴DE是⊙O的切线;
(2)、设半径为r,则OE=AE﹣OA=6﹣r,OC=r,在Rt△OCE中,∵OC2+CE2=OE2,
∴r2+(2![]() )2=(6﹣r)2,解得r=2,∵tan∠COE=
)2=(6﹣r)2,解得r=2,∵tan∠COE=![]() =
=![]() =
=![]() ,∴∠COE=60°,
,∴∠COE=60°,
∴S阴影部分=S△COE﹣S扇形BOC=![]() ×2×2
×2×2![]() ﹣
﹣![]() =2
=2![]() ﹣
﹣![]() π.
π.

练习册系列答案
相关题目