题目内容
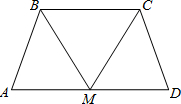
（1）解方程：x2-4x-1=0；（2）如图所示，在梯形ABCD中，BC∥AD，AB=DC，点M是AD的中点．求证：BM=CM．
分析：（1）利用求根公式进行求解即可；
（2）根据等腰梯形的性质得出∠A=∠D，根据SAS证出△BAM≌△CDM即可．
（2）根据等腰梯形的性质得出∠A=∠D，根据SAS证出△BAM≌△CDM即可．
解答：解：（1）根据求根公式可得：x1=
=2+
，x2=
=2-
；
（2）证明：∵等腰梯形ABCD，BC∥AD，AB=CD，
∴∠A=∠D，
∵点M是AD中点，
∴AM=DM，
在△BAM和△CDM中，
，
∴△BAM≌△CDM，
∴BM=CM．
4+
| ||
| 2 |
| 5 |
4-
| ||
| 2 |
| 5 |
（2）证明：∵等腰梯形ABCD，BC∥AD，AB=CD，
∴∠A=∠D，
∵点M是AD中点，
∴AM=DM，
在△BAM和△CDM中，
|
∴△BAM≌△CDM，
∴BM=CM．
点评：本题考查了等腰梯形的性质和全等三角形的性质和判定的应用，关键是求出△BAM≌△CDM，题目比较典型，难度不大．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
相关题目