题目内容
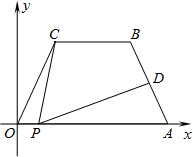 如图所示,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,点P不与点0、点A重合.连接CP,过点P作PD交AB于点D.
如图所示,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,点P不与点0、点A重合.连接CP,过点P作PD交AB于点D.(1)求点B的坐标;
(2)当点P运动什么位置时,△OCP为等腰三角形,求这时点P的坐标;
(3)当点P运动什么位置时,使得∠CPD=∠OAB,且
| BD |
| BA |
| 5 |
| 8 |
分析:(1)过B作BQ⊥OA于Q易得∠COA=∠BAQ=60°,在Rt△BQA中,根据三角函数的定义可得QB的长,进而可得OQ的长;即可得B的坐标;
(2)分点P在x正半轴上与x负半轴上上两种情况讨论,结合等腰三角形的性质,可得OP、OC的长,进而可得答案;
(3)根据题意易得△COP∽△PAD,进而可得比例关系
=
,代入数据可得答案.
(2)分点P在x正半轴上与x负半轴上上两种情况讨论,结合等腰三角形的性质,可得OP、OC的长,进而可得答案;
(3)根据题意易得△COP∽△PAD,进而可得比例关系
| OP |
| AD |
| OC |
| AP |
解答: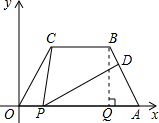 解:(1)过B作BQ⊥OA于Q,则∠COA=∠BAQ=60°,
解:(1)过B作BQ⊥OA于Q,则∠COA=∠BAQ=60°,
在Rt△BQA中,QB=ABsin60°=2
,
QA=
=
=2,
∴OQ=OA-QA=7-2=5.
∴B(5,2
).
(2)①当OC=OP时,若点P在x正半轴上,
∵∠COA=60°,△OCP为等腰三角形,
∴△OCP是等边三角形.
∴OP=OC=CP=4.
∴P(4,0).
若点P在x负半轴上,
∵∠COA=60°,
∴∠COP=120°.
∴△OCP为顶角120°的等腰三角形.
∴OP=OC=4.
∴P(-4,0)
∴点P的坐标为(4,0)或(-4,0).
②当OC=CP时,由题意可得C的横坐标为:4×cos60°=2,
∴P点坐标为(4,0)
③当OP=CP时,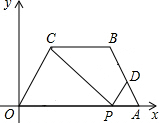
∵∠COA=60°,
∴△OPC是等边三角形,同①可得出P(4,0).
综上可得点P的坐标为(4,0)或(-4,0).
(3)∵∠CPD=∠OAB=∠COP=60°,
∴∠OPC+∠DPA=120°.
又∵∠PDA+∠DPA=120°,
∴∠OPC=∠PDA.
∵∠COP=∠A=60°,
∴△COP∽△PAD.
∴
=
.
∵
=
,AB=4,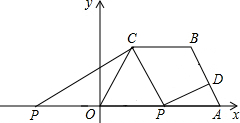
∴BD=
,
AD=
.
即
=
.
∴7OP-OP2=6得OP=1或6.
∴P点坐标为(1,0)或(6,0).
 解:(1)过B作BQ⊥OA于Q,则∠COA=∠BAQ=60°,
解:(1)过B作BQ⊥OA于Q,则∠COA=∠BAQ=60°,在Rt△BQA中,QB=ABsin60°=2
| 3 |
QA=
| AB2-BQ2 |
42-(2
|
∴OQ=OA-QA=7-2=5.
∴B(5,2
| 3 |
(2)①当OC=OP时,若点P在x正半轴上,
∵∠COA=60°,△OCP为等腰三角形,
∴△OCP是等边三角形.
∴OP=OC=CP=4.
∴P(4,0).
若点P在x负半轴上,
∵∠COA=60°,
∴∠COP=120°.
∴△OCP为顶角120°的等腰三角形.
∴OP=OC=4.
∴P(-4,0)
∴点P的坐标为(4,0)或(-4,0).
②当OC=CP时,由题意可得C的横坐标为:4×cos60°=2,
∴P点坐标为(4,0)
③当OP=CP时,

∵∠COA=60°,
∴△OPC是等边三角形,同①可得出P(4,0).
综上可得点P的坐标为(4,0)或(-4,0).
(3)∵∠CPD=∠OAB=∠COP=60°,
∴∠OPC+∠DPA=120°.
又∵∠PDA+∠DPA=120°,
∴∠OPC=∠PDA.
∵∠COP=∠A=60°,
∴△COP∽△PAD.
∴
| OP |
| AD |
| OC |
| AP |
∵
| BD |
| AB |
| 5 |
| 8 |

∴BD=
| 5 |
| 2 |
AD=
| 3 |
| 2 |
即
| OP | ||
|
| 4 |
| 7-OP |
∴7OP-OP2=6得OP=1或6.
∴P点坐标为(1,0)或(6,0).
点评:本题是一道动态几何压轴题,对学生的分类思想作了重点的考查,是一道很不错的题.

练习册系列答案
相关题目
 交于点A,过点A分别作x轴、y轴的垂线,垂足为点B、C.如果四边形OBAC是正方形,求一次函数的关系式.
交于点A,过点A分别作x轴、y轴的垂线,垂足为点B、C.如果四边形OBAC是正方形,求一次函数的关系式. 5、如图所示,在平面直角坐标系中,点A、B的坐标分别为(-2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A′的坐标为( )
5、如图所示,在平面直角坐标系中,点A、B的坐标分别为(-2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A′的坐标为( ) 如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次从点P跳到关于点A的对称点M处,第二次从点M跳到关于点B的对称点N处,第三次从点N跳到关于点C的对称点处,…如此下去.
如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次从点P跳到关于点A的对称点M处,第二次从点M跳到关于点B的对称点N处,第三次从点N跳到关于点C的对称点处,…如此下去. 如图所示,在平面直角坐标系xoy中,有一组对角线长分别为1,2,3的正方形A1B1C1O、A2B2C2B1、A3B3C3B2,其对角线OB1、B1B2、B2 B3依次放置在y轴上(相邻顶点重合),依上述排列方式,对角线长为n的第n个正方形的顶点An的坐标为
如图所示,在平面直角坐标系xoy中,有一组对角线长分别为1,2,3的正方形A1B1C1O、A2B2C2B1、A3B3C3B2,其对角线OB1、B1B2、B2 B3依次放置在y轴上(相邻顶点重合),依上述排列方式,对角线长为n的第n个正方形的顶点An的坐标为 BE.
BE.