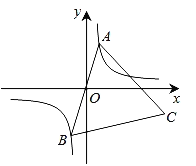
题目内容
【题目】有一块直角三角形绿地,量得两直角边长分别为3m,4m,现在要将绿地扩充成等腰三角形,且扩充时只能延长两条直角边中的一条,则扩充后等腰三角形绿地的面积为m2 .
【答案】8或10或12或 ![]() 或
或 ![]()
【解析】解:①如图1: 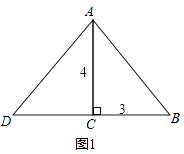
当BC=CD=3m时;
由于AC⊥BD,则AB=AD=5m;
此时等腰三角形绿地的面积: ![]() ×6×4=12(m2);
×6×4=12(m2);
②如图2: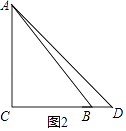
当AC=CD=4m时;
∵AC⊥CB,
此时等腰三角形绿地的面积: ![]() ×4×4=8(m2);
×4×4=8(m2);
③图3: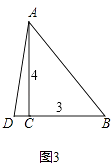
当AD=BD时,设AD=BD=xm;
Rt△ACD中,BD=xm,CD=(x﹣3)m;
由勾股定理,得AD2=DC2+CA2 , 即(x﹣3)2+42=x2 ,
解得x= ![]() ;
;
此时等腰三角形绿地的面积: ![]() ×BD×AC=
×BD×AC= ![]() ×
× ![]() ×4=
×4= ![]() (m2).
(m2).
④如图4,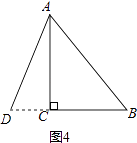
延长BC到D使BD等于5m,
此时AB=BD=5m,
故CD=2m,![]() BDAC=
BDAC= ![]() ×5×4=10(m2).
×5×4=10(m2).
⑤如图5,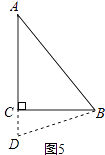
延长AC到D使AD等于5m,
此时AB=AD=5m,
故BC=3m,![]() BCAD=
BCAD= ![]() ×5×3=
×5×3= ![]() (m2).
(m2).
所以答案是:8或10或12或 ![]() 或
或 ![]() .
.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
【题目】某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示: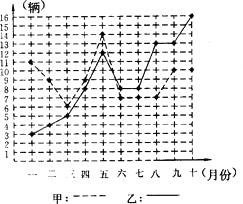
(1)请你根据上图填写下表.
销售公司 | 平均数 | 方差 | 中位数 | 众数 |
甲 | 9 | |||
乙 | 9 | 17.0 | 8 |
(2)请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:①从平均数和方差结合看;②从折线图上甲、乙两个汽车销售公司销售数量的趋势看(分析哪个汽车销售公司较有潜力).