题目内容
【题目】如图,已知:△ABC在正方形网格中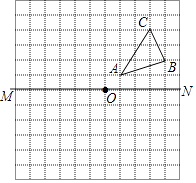
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于点O对称的△A2B2C2;
(3)在直线MN上求作一点P,使△PAB的周长最小,请画出△PAB.
【答案】
(1)解:△A1B1C1如图所示;
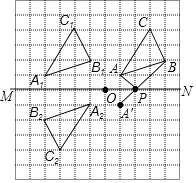
(2)解:△A2B2C2如图所示;

(3)解:△PAB如图所示.

【解析】(1)根据网格结构找出点A、B、C向左平移5个单位长度后的对应点A1、B1、C1的位置,然后顺次连接即可;
(2)根据网格结构找出点A、B、C关于点O对称的点A2、B2、C2的位置,然后顺次连接即可;
(3)找出点A关于直线MN的对称点A′的位置,连接A′B与直线MN相交于点P,根据轴对称确定最短路线问题,点P即为所求的点.
【考点精析】通过灵活运用线段的基本性质和轴对称图形,掌握线段公理:所有连接两点的线中,线段最短.也可简单说成:两点之间线段最短;连接两点的线段的长度,叫做这两点的距离;线段的大小关系和它们的长度的大小关系是一致的;两个完全一样的图形关于某条直线对折,如果两边能够完全重合,我们就说这两个图形成轴对称,这条直线就对称轴即可以解答此题.

练习册系列答案
相关题目