题目内容
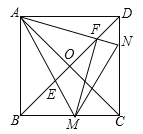
【题目】如图,正方形ABCD的对角线相交于点O,点M,N分别是边BC,CD上的动点(不与点B,C,D重合),AM,AN分别交BD于点E,F,且∠MAN始终保持45°不变.
(1)求证:![]() =
=![]() ;
;
(2)求证:AF⊥FM;
(3)请探索:在∠MAN的旋转过程中,当∠BAM等于多少度时,∠FMN=∠BAM?写出你的探索结论,并加以证明.

【答案】(1)详见解析;(2)详见解析;(3)∠BAM=22.5时,∠FMN=∠BAM,理由详见解析.
【解析】
试题分析:(1)根据已知易证∠MAF=∠MBE,即可得A、B、M、F四点共圆,根据圆内接四边形对角互补可求得∠AFM=90°,根据等腰直角三角形性质即求得![]() =
=![]() ;(2)由(1)的结论∠AFM=90°,即可得AF⊥FM;.(3)由A、B、M、F四点共圆,可证得∠BAM=∠EFM,因为∠BAM=∠FMN,所以∠EFM=∠FMN,推出MN∥BD,得到
;(2)由(1)的结论∠AFM=90°,即可得AF⊥FM;.(3)由A、B、M、F四点共圆,可证得∠BAM=∠EFM,因为∠BAM=∠FMN,所以∠EFM=∠FMN,推出MN∥BD,得到![]() =
=![]() ,推出BM=DN,再证明△ABM≌△ADN即可解决问题.
,推出BM=DN,再证明△ABM≌△ADN即可解决问题.
试题解析:
(1)证明:∵四边形ABCD是正方形,
∴∠ABD=∠CBD=45°,∠ABC=90°,
∵∠MAN=45°,
∴∠MAF=∠MBE,
∴A、B、M、F四点共圆,
∴∠ABM+∠AFM=180°,
∴∠AFM=90°,
∴∠FAM=∠FMA=45°,
∴AM=![]() AF,
AF,
∴![]() =
=![]() .
.
(2)由(1)可知∠AFM=90°,
∴AF⊥FM.
(3)结论:∠BAM=22.5时,∠FMN=∠BAM
理由:∵A、B、M、F四点共圆,
∴∠BAM=∠EFM,
∵∠BAM=∠FMN,
∴∠EFM=∠FMN,
∴MN∥BD,
∴![]() =
=![]() ,∵CB=DC,
,∵CB=DC,
∴CM=CN,
∴MB=DN,
在△ABM和△ADN中,
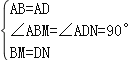 ,
,
∴△ABM≌△ADN,
∴∠BAM=∠DAN,
∵∠MAN=45°,
∴∠BAM+∠DAN=45°,
∴∠BAM=22.5°.