Question

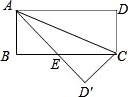如图，在矩形ABCD中，AB=5，BC=12，将矩形ABCD沿对角线对折，然后放在桌面上，折叠后所成的图形覆盖桌面的面积是

 

．

Answer 1

分析：由图形可知：折叠后所成的图形覆盖桌面的面积是原矩形的面积减去重合的部分的面积，只要求出重合的部分的面积即三角形AEC的面积即可，利用勾股定理求出EC答案可得．

解答：解：设折叠后所成圆形覆盖桌面的面积为S，则：

S=S△ABC+S△AD1C-S△AEC=S矩形ABCD-S△AEC S△AEC= 1 2 AB•EC= 5 2 EC

，
由Rt△ABE≌Rt△CD₁E知EC=AE，
设EC=x，则AB²+BE²=x²，
即5²+（12-x）²=x²，
解得：x=

169

24

S△AEC=

5

2

×

169

24

=

845

48

S=5×12-

845

48

=

2035

48

，
故答案为：

2035

48

．

点评：本题考查了图形的翻折问题、三角形的面积及勾股定理；利用勾股定理求得EC的大小，从而求得重合部分的面积是正确解答本题的关键．