Question

【题目】如图,PA=PB,∠1+∠2=180°.求证:OP平分∠AOB.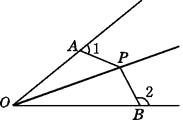

Answer 1

【答案】证明:过点P作PE⊥AO,PF⊥OB,垂足分别为E,F,则∠AEP=∠BFP=90°.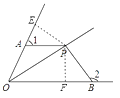

∵∠1+∠2=180°,∠2+∠PBO=180°,
∴∠1=∠PBO.
在△PAE和△PBF中,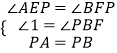
∴△PAE≌△PBF(AAS).
∴PE=PF.
∴OP为∠AOB的平分线,即OP平分∠AOB.
【解析】过点P作PE⊥AO,PF⊥OB,垂足分别为E,F,则∠AEP=∠BFP=90°. 根据邻补角的定义得出∠2+∠PBO=180°,又因∠1+∠2=180°，根据同角的补角相等得出∠1=∠PBO.然后根据AAS判断出△PAE≌△PBF，根据全等三角形对应角相等得出PE=PF.根据到角两边距离相等的点在这个角的角平分线上得出OP为∠AOB的平分线,即OP平分∠AOB.