��Ŀ����
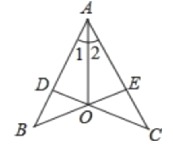
����Ŀ����ͼ��������ABCD�У���MAN=45�㣬��MAN�Ƶ�A˳ʱ����ת���������߷ֱ�CB��DC�������ǵ��ӳ��ߣ��ڵ�M��N.����MAN�Ƶ�A��ת��BM=DNʱ����ͼ1������֤BM+DN=MN.
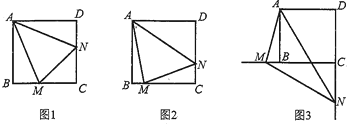
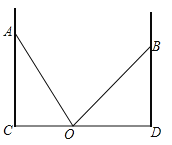
��1������MAN�Ƶ�A��ת��BM��DNʱ����ͼ2),�߶�BM��DN��MN֮����������������ϵ��д������.������֤��.
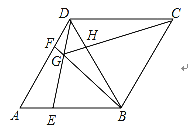
��2������MAN�Ƶ�A��ת����ͼ3λ��ʱ,�߶�BM��DN��MN֮����������������ϵ����д����IJ��룬������֤��.
���𰸡���1��MN=BM+DN��֤���ԣ���2��MN=DN-BM��֤����.
��������
��1��BM+DN=MN������֤��B��E��M���㹲���ɵõ���AEM�ա�ANM���Ӷ�֤��ME=MN��
��2��DN-BM=MN��֤�������루1�����ƣ�����⣮
�⣺��1��BM+DN=MN������
֤����֤�����£���ͼ2����MB���ӳ����ϣ���ȡBE=DN������AE��
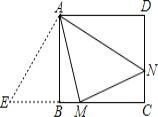
����ABE����ADN��
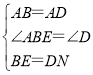 ��
��
���ABE�ա�ADN��SAS����
��AE=AN����EAB=��NAD��
�ߡ�BAD=90������MAN=45����
���BAM+��DAN=45����
���EAB+��BAM=45����
���EAM=��NAM��
����AEM����ANM��
 ��
��
���AEM�ա�ANM��SAS����
��ME=MN��
��ME=BE+BM=DN+BM��
��DN+BM=MN��
��2�����ۣ�DN-BM=MN��
���߶�DN�Ͻ�ȡDQ=BM��
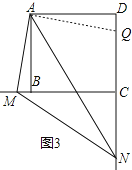
����ADQ����ABM��
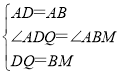 ��
��
���ADQ�ա�ABM��SAS����
���DAQ=��BAM��
���QAN=��MAN��
����AMN����AQN��
 ��
��
���AMN�ա�AQN��SAS����
��MN=QN��
��DN-BM=MN��