Question

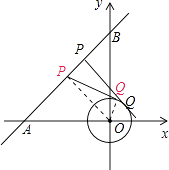
【题目】如图，在平面直角坐标系xOy中，直线AB经过点A（﹣4，0）、B（0，4），⊙O的半径为1（O为坐标原点），点P在直线AB上，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为 ．

Answer 1

【答案】
【解析】解：连接OP、OQ． ∵PQ是⊙O的切线，
∴OQ⊥PQ；
根据勾股定理知PQ2=OP2﹣OQ2 ，
∵当PO⊥AB时，线段PQ最短；
又∵A（﹣4，0）、B（0，4），
∴OA=OB=4，
∴AB=4
∴OP= AB=2 ，
∴PQ= ；
所以答案是： ．

【考点精析】通过灵活运用等腰直角三角形和垂线段最短，掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；连接直线外一点与直线上各点的所有线段中，垂线段最短；现实生活中开沟引水，牵牛喝水都是“垂线段最短”性质的应用即可以解答此题．