Question

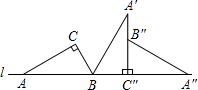如图，把直角三角形ABC的斜边AB放在定直线l上，按顺时针方向在l上转动两次，使它转到△A″B″C″的位置．若BC=1，AC=

3

，则顶点A运动到点A″的位置时，点A两次运动所经过的路程

 

．（计算结果不取近似值）

Answer 1

分析：根据题意得到直角三角形在直线l上转动两次点A分别绕点B旋转120°和绕C″旋转90°，将两条弧长求出来加在一起即可．

解答：解：在Rt△ABC中，
∵BC=1，AC=

3

，
∴AB=2，∠CBA=60°，
∴弧AA′=

120π×2

180

=

4

3

π，
弧A′A′′=

90π× 3

180

=

3

2

π，
∴点A经过的路线的长是

4

3

π+

3

2

π．
故答案为：(

4

3

+

3

2

)π．

点评：本题考查了弧长的计算方法及勾股定理，解题的关键是根据直角三角形的转动过程判断点A是以那一点为圆心转动多大的角度．