题目内容
 如图,圆锥的底面半径OA=2cm,高为PO=4
如图,圆锥的底面半径OA=2cm,高为PO=4| 2 |
分析:沿PA剪开展开后得出扇形PAA′,连接AA′交PB于N,连接AM,则AM的长为蚂蚁爬行的最短路程由勾股定理求出PA=PB=6(cm),求出弧AB的长,求出弧AB对的圆心角,在Rt△PNA中,求出PN=3,AN=3
,求出PM=BM=
PB=3cm,即可得出M和N重合,得出即可.
| 3 |
| 1 |
| 2 |
解答:
解:沿PA剪开展开后得出扇形PAA′,连接AA′交PB于N,连接AM,则AM的长为蚂蚁爬行的最短路程,
∵由勾股定理得:PA=PB=
=
=6(cm),
∴弧AB=
×(2π×2)=2π(cm),
∴弧AB对的圆心角是
=
π=60°,
∴在Rt△PNA中,PN=PA•cos60°=3cm,AN=PA•sin60°=3
(cm),
∵M为PB中点,
∴PM=BM=
PB=
×6cm=3cm,
即M和N重合,
∴AM=AN=3
cm,
故选A.

解:沿PA剪开展开后得出扇形PAA′,连接AA′交PB于N,连接AM,则AM的长为蚂蚁爬行的最短路程,
∵由勾股定理得:PA=PB=
| AO2+PO2 |
22+(4
|
∴弧AB=
| 1 |
| 2 |
∴弧AB对的圆心角是
| 2π |
| 6 |
| 1 |
| 3 |
∴在Rt△PNA中,PN=PA•cos60°=3cm,AN=PA•sin60°=3
| 3 |
∵M为PB中点,
∴PM=BM=
| 1 |
| 2 |
| 1 |
| 2 |
即M和N重合,
∴AM=AN=3
| 3 |
故选A.
点评:本题考查了解直角三角形,勾股定理,求弧长公式,最短路线问题的应用,主要考查学生的计算能力.

练习册系列答案
相关题目
 如图,圆锥的底面半径为1,侧面积为3π,则这个圆锥的母线长是( )
如图,圆锥的底面半径为1,侧面积为3π,则这个圆锥的母线长是( )| A、0.5 | B、1 | C、2 | D、3 |
 如图,圆锥的底面半径为3cm,高为4cm,那么这个圆锥的侧面积是( )
如图,圆锥的底面半径为3cm,高为4cm,那么这个圆锥的侧面积是( )| A、10πcm2 | B、15πcm2 | C、20πcm2 | D、25πcm2 |
 如图,圆锥的底面半径为5,母线长为20,一只蜘蛛从底面圆周上一点A出发沿圆锥的侧面爬行一周后回到点A的最短路程是( )
如图,圆锥的底面半径为5,母线长为20,一只蜘蛛从底面圆周上一点A出发沿圆锥的侧面爬行一周后回到点A的最短路程是( )| A、8 | ||
B、10
| ||
C、15
| ||
D、20
|
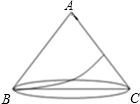 如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上,问它爬行的最短路线是多少?
如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上,问它爬行的最短路线是多少? (2013•增城市二模)如图,圆锥的底面半径OB=6cm,高OC=8cm.则这个圆锥的侧面积是( )
(2013•增城市二模)如图,圆锥的底面半径OB=6cm,高OC=8cm.则这个圆锥的侧面积是( )