题目内容
 如图,圆锥的底面半径为5,母线长为20,一只蜘蛛从底面圆周上一点A出发沿圆锥的侧面爬行一周后回到点A的最短路程是( )
如图,圆锥的底面半径为5,母线长为20,一只蜘蛛从底面圆周上一点A出发沿圆锥的侧面爬行一周后回到点A的最短路程是( )| A、8 | ||
B、10
| ||
C、15
| ||
D、20
|
分析:易得圆锥的底面周长也就是圆锥的侧面展开图的弧长,利用弧长公式即可求得侧面展开图的圆心角,进而构造直角三角形求得相应线段即可.
解答:解:圆锥的底面周长=2π×5=10π,
设侧面展开图的圆心角的度数为n.
∴
=10π,
解得n=90,
圆锥的侧面展开图,如图所示:
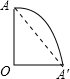
∴最短路程为:
=20
,故选D.
设侧面展开图的圆心角的度数为n.
∴
| nπ×20 |
| 180 |
解得n=90,
圆锥的侧面展开图,如图所示:

∴最短路程为:
| 202+202 |
| 2 |
点评:求立体图形中两点之间的最短路线长,一般应放在平面内,构造直角三角形,求两点之间的线段的长度.用到的知识点为:圆锥的弧长等于底面周长.

练习册系列答案
相关题目
 如图,圆锥的底面半径为1,侧面积为3π,则这个圆锥的母线长是( )
如图,圆锥的底面半径为1,侧面积为3π,则这个圆锥的母线长是( )| A、0.5 | B、1 | C、2 | D、3 |
 如图,圆锥的底面半径为3cm,高为4cm,那么这个圆锥的侧面积是( )
如图,圆锥的底面半径为3cm,高为4cm,那么这个圆锥的侧面积是( )| A、10πcm2 | B、15πcm2 | C、20πcm2 | D、25πcm2 |
 如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上,问它爬行的最短路线是多少?
如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上,问它爬行的最短路线是多少? (2013•增城市二模)如图,圆锥的底面半径OB=6cm,高OC=8cm.则这个圆锥的侧面积是( )
(2013•增城市二模)如图,圆锥的底面半径OB=6cm,高OC=8cm.则这个圆锥的侧面积是( )