题目内容
 如图,线段AB,C是AB上一点,M是AC的中点,N是BC的中点
如图,线段AB,C是AB上一点,M是AC的中点,N是BC的中点(1)若线段AB=10cm,BC=4cm,求MN的长;
(2)猜想MN=
分析:(1)因为线段AB=10cm,BC=4cm,故知AC=6,又知M是AC的中点,N是BC的中点,即可求出MN的长;
(2)因为M是AC的中点,N是BC的中点,则MC=
AC,CN=
BC,故MN=MC+CN=
AB可求.
(2)因为M是AC的中点,N是BC的中点,则MC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵线段AB=10cm,BC=4cm,
∴AC=6cm,
∵M是AC的中点,N是BC的中点,
∴MN=
AB=5;
(2)猜想MN=
AB,
∵M是AC的中点,N是BC的中点,
∴MN=MC+CN=
AC+
BC=
AB.
∴AC=6cm,
∵M是AC的中点,N是BC的中点,
∴MN=
| 1 |
| 2 |
(2)猜想MN=
| 1 |
| 2 |
∵M是AC的中点,N是BC的中点,
∴MN=MC+CN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查比较线段的长短的知识点,能够根据中点的概念,用几何式子表示线段的关系,还要注意线段的和差表示方法.

练习册系列答案
相关题目
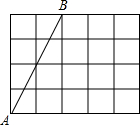 如图,线段AB的端点是4×5的正方形网格的格点,若再在网格的格点中取一点C,使△ABC成为等腰三角形,则符合条件的点C的个数是( )
如图,线段AB的端点是4×5的正方形网格的格点,若再在网格的格点中取一点C,使△ABC成为等腰三角形,则符合条件的点C的个数是( )| A、1个 | B、2个 | C、3个 | D、4个 |
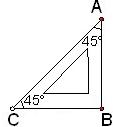 24、如图,线段
24、如图,线段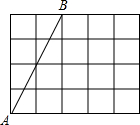 如图,线段AB的端点是4×5的正方形网格的格点,若再在网格的格点中取一点C,使△ABC成为等腰三角形,则符合条件的点C的个数是
如图,线段AB的端点是4×5的正方形网格的格点,若再在网格的格点中取一点C,使△ABC成为等腰三角形,则符合条件的点C的个数是 如图,线段AB,C是AB上一点,M是AC的中点,N是BC的中点
如图,线段AB,C是AB上一点,M是AC的中点,N是BC的中点