题目内容
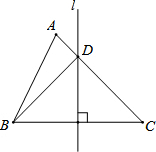
如图,在等腰△ABC中,∠BAC=120°,DE是AC的垂直平分线,DE=1cm,求BD的长.
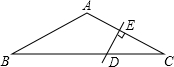

如图,连接AD,
∵等腰△ABC中,∠BAC=120°,
∴∠B=∠C=
(180°-120°)=30°,
∵DE是AC的垂直平分线,
∴AD=CD,
∴∠DAC=∠C=30°,
∴∠BAD=∠BAC-∠DAC=120°-30°=90°,
在Rt△CDE中,∵DE=1cm,
∴CD=2DE=2cm,
在Rt△ABD中,BD=2AD=2CD=2×2=4cm.
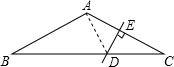
∵等腰△ABC中,∠BAC=120°,
∴∠B=∠C=
| 1 |
| 2 |
∵DE是AC的垂直平分线,
∴AD=CD,
∴∠DAC=∠C=30°,
∴∠BAD=∠BAC-∠DAC=120°-30°=90°,
在Rt△CDE中,∵DE=1cm,
∴CD=2DE=2cm,
在Rt△ABD中,BD=2AD=2CD=2×2=4cm.


练习册系列答案
相关题目
某校为了更好地开展“阳光体育一小时”活动,围绕着“你最喜欢的体育活动项目是什么(只写一项)?”的问题,对本校学生进行了随机抽样调查,以下是根据得到的相关数据绘制的统计图的一部分.

各年级学生人数统计表
年级 | 七年级 | 八年级 | 九年级 |
学生人数 | 180 | 120 |
|
请根据以上信息解答下列问题:
(1)该校对多少名学生进行了抽样调查?
(2)请将图1和图2补充完整;
(3)已知该校七年级学生比九年级学生少20人,请你补全上表,并利用样本数据估计全校学生中最喜欢踢毽子运动的人数约为多少?