题目内容

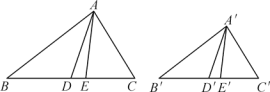
【题目】如图，△A′B′C′∽△ABC，且A′E′，AE是角平分线，A′D′，AD是中线．求证：△A′D′E′∽△ADE.

【答案】见解析

【解析】

根据△A′B′C′∽△ABC，可以得到中线及高的比都等与相似比，且∠B′＝∠B，又因为中线的定义得＝，从而得到△A′B′D′∽△ABD，及∠B′A′D′＝∠BAD，最终得到△A′D′E′∽△ADE.

∵A′D′，AD是两个三角形的中线，A′E′，AE是两个三角形的角平分线，△A′B′C′∽△ABC，∴＝，＝，∴＝，又∵△A′B′C′∽△ABC，∴∠B′＝∠B，＝，又点D，点D′为BD，B′D′中点，∴B′D′＝B′C′，BD＝BC，∴＝，∴△A′B′D′∽△ABD，∴∠B′A′D′＝∠BAD，∴∠D′A′E′＝∠DAE，∴△A′D′E′∽△ADE

练习册系列答案
相关题目

【题目】在一块长方形镜面玻璃的四周镶上与它的周长相等的边框，制成一面镜子，镜子的长与宽的比是2：1，已知镜面玻璃的价格是每平方米120元，边框的价格是每米30元，另外制作这面镜子还需加工费45元．设制作这面镜子的总费用是元，镜子的宽是米．

（1）求与之间的关系式．

（2）如果制作这面镜子共花了195元，求这面镜子的长和宽．

【题目】如图，在平面直角坐标系xOy中，以点O为圆心的圆分别交x轴的正半轴于点M，交y轴的正半轴于点N．劣弧的长为，直线与x轴、y轴分别交于点A、B．

（1）求证：直线AB与⊙O相切；

（2）求图中所示的阴影部分的面积（结果用π表示）

【题目】某数学社团成员想利用所学的知识测量某广告牌的宽度图中线段MN的长，直线MN垂直于地面，垂足为点在地面A处测得点M的仰角为、点N的仰角为，在B处测得点M的仰角为，米，且A、B、P三点在一直线上请根据以上数据求广告牌的宽MN的长．

参考数据：，，，，，

【题目】如图所示，的直径，点是延长线上的一点，过点作的切线，切点为，连接.

（1）若，求的长；

（2）若点在的延长线上运动，的平分线交于点，你认为的大小是否发生变化？若变化，请说明理由；若不变化，求出的大小.

【题目】为了提倡“保护自然资源，节约自然资源”，某部门对某县一次性筷子的用量进行了调查.2015年从该县600家高、中、低档饭店中抽取了10家进行调查，得知这些饭店每天消耗的一次性筷子的盒数分别为：0.6，3.7，2.2，1.5，2.8，1.7，1.2，2.1，3.2，1.0.

(1)估计该县2015年各饭店共消耗多少盒一次性筷子？(一年按350个营业日计算)

(2)在(1)的条件下，若生产一套学生课桌椅需木材0.07 m3，则该县2015年各饭店使用一次性筷子所消耗的木材可以生产多少套学生课桌椅？(计算中需用到的有关数据为：每盒筷子100双，每双筷子的质量为5 g，所用木材的密度为0.5×103 kg/m3)

(3)通过以上计算，你对保护自然资源有什么看法？请提出两条合理的看法．

【题目】在△ABC中，∠ACB＝90°，点D、E分别在边BC、AC上，AC＝3AE，∠CDE＝45°（如图），△DCE沿直线DE翻折，翻折后的点C落在△ABC内部的点F，直线AF与边BC相交于点G，如果BG＝AE，那么tanB＝_____．

【题目】二次函数y＝ax2﹣2ax﹣3（a≠0）的图象经过点A．

（1）求二次函数的对称轴；

（2）当A（﹣1，0）时，

①求此时二次函数的表达式；

②把y＝ax2﹣2ax﹣3化为y＝a（x﹣h）2+k的形式，并写出顶点坐标；

③画出函数的图象．

【题目】如图，在平面直角坐标系xOy中，A（0，3），B（1，0），连接BA，将线段BA绕点B顺时针旋转90°得到线段BC，反比例函数y＝的图象G经过点C．

（1）请直接写出点C的坐标及k的值；

（2）若点P在图象G上，且∠POB＝∠BAO，求点P的坐标；

（3）在（2）的条件下，若Q（0，m）为y轴正半轴上一点，过点Q作x轴的平行线与图象G交于点M，与直线OP交于点N，若点M在点N左侧，结合图象，直接写出m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网