��Ŀ����
����Ŀ����ͼ��գ���ע�����ɣ�
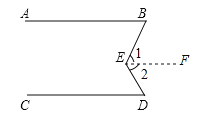
�������ȷ��֤������ͼ����֪AB��CD����֤����BED=��B+��D
֤������E����EF��AB������ֱ����һ������ֻ��һ��ֱ��������ֱ��ƽ�У�
���1= �� ��
��AB��CD����֪��
��EF��CD���������ֱ����ͬһֱ��ƽ�У���ô����Ҳƽ�У�
���2= �� ��
�֡�BED=��1+��2
���BED=��B+��D ��������������
����ͼ���ڡ�ABC�У�EF��AD����1=��2����BAC=70�㣮�����AGD�Ĺ�����д������
�⣺��ΪEF��AD����֪��
���ԡ�2=��3���� ��
����Ϊ��1=��2�����ԡ�1=��3��������������
����AB�� �� ��
���ԡ�BAC+ =180�㣨 ����
����Ϊ��BAC=70�㣬���ԡ�AGD=110�㣮

ͼ�� ͼ��
���𰸡�(1) ��B ����ֱ��ƽ�У��ڴ�����ȣ�
��D ����ֱ��ƽ�У��ڴ�����ȣ�
(2) ����ֱ��ƽ�У�ͬλ����ȣ���
DG ���ڴ�����ȣ���ֱ��ƽ�У���
��AGD ����ֱ��ƽ�У�ͬ���ڽǻ�����
����������������1������ƽ���ߵ����ʽ�����⣻��2������ƽ���ߵ��ж���������⣮
���������
֤������E����EF��AB������ֱ����һ������ֻ��һ��ֱ��������ֱ��ƽ�У�
���1= ��B ����ֱ��ƽ�У��ڴ�����ȣ�
��AB��CD����֪��
��EF��CD���������ֱ����ͬһֱ��ƽ�У���ô����Ҳƽ�У�
���2= ��D ����ֱ��ƽ�У��ڴ�����ȣ�
�֡�BED=��1+��2
���BED=��B+��D ��������������
����ͼ���ڡ�ABC�У�EF��AD����1=��2����BAC=70�㣮�����AGD�Ĺ�����д������
�⣺��ΪEF��AD����֪��
���ԡ�2=��3������ֱ��ƽ�У�ͬλ����ȣ�
����Ϊ��1=��2�����ԡ�1=��3��������������
����AB�� DG ���ڴ�����ȣ���ֱ��ƽ�У�
���ԡ�BAC+ ��AGD =180�㣨��ֱ��ƽ�У�ͬ���ڽǻ�������
����Ϊ��BAC=70�㣬���ԡ�AGD=110�㣮