题目内容
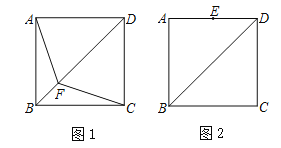
【题目】已知:如图,正方形ABCD中,点F是对角线BD上的一个动点.
(1)如图1,连接AF,CF,直接写出AF与CF的数量关系;
(2)如图2,点E为AD边的中点,当点F运动到线段EC上时,连接AF,BE相交于点O.
①请你根据题意在图2中补全图形;
②猜想AF与BE的位置关系,并写出证明此猜想的思路;
③如果正方形的边长为2,直接写出AO的长.
【答案】(1)AF=CF(2)① 图形见解析②![]() ③
③![]() .
.
【解析】试题分析:(1)根据正方形的对称性即可得结论;(2)①根据题意,补全图形即可;②AF⊥BE,由四边形ABCD是正方形,可得AD=CD,∠ADB=∠CDB.进而可得ΔADF≌ΔCDF.从而得到1=∠2;由E为正方形ABCD的AD边的中点,可证ΔABE≌ΔDCE.从而得到∠3=∠4;由∠2+∠4=90°可知∠1+∠3=90°,进而可得∠AOE=90°,即AF⊥BE.③根据勾股定理可得BE=![]() ,因AF⊥BE,根据
,因AF⊥BE,根据![]() ,即可求得AO的长.
,即可求得AO的长.
试题解析:
(1)解:AF=CF.
(2)解:① 补全图形:
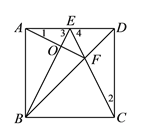
②![]() .
.
证明思路如下:
(i)由四边形ABCD是正方形,
可得AD=CD,∠ADB=∠CDB.
进而可得![]() ≌
≌![]() .从而得到1=∠2.
.从而得到1=∠2.
(ii)由E为正方形ABCD的AD边的中点,可证![]() ≌
≌![]() .
.
从而得到∠3=∠4.
(iii)由∠2+∠4=90°可知∠1+∠3=90°,进而可得∠AOE=90°.
即![]() .
.
③![]() .
.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目