题目内容
如图所示,有一个可以自由转动的圆形转盘,被平均分成四个扇形,四个扇形内分别标有数字1、2、-3、-4.若将转盘转动两次,每一次停止转动后,指针指向的扇形内的数字分别记为a、b(若指针恰好指在分界线上,则该次不计,重新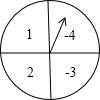 转动一次,直至指针落在扇形内).
转动一次,直至指针落在扇形内).(1)若将转盘只转动一次,指针指向的扇形内的数字为负数的概率是
(2)请你用列表法或树状图求a与b的乘积等于2的概率;
(3)求a、b能使一元二次方程x2+ax-b=0有实数根的概率.
分析:(1)让负数的个数除以数的总个数即可;
(2)a与b的乘积等于2的情况数除以总情况数即为所求的概率;
(3)找到△≥0的情况数占总情况数的多少即可.
(2)a与b的乘积等于2的情况数除以总情况数即为所求的概率;
(3)找到△≥0的情况数占总情况数的多少即可.
解答:解:(1)2÷4=
,故答案为
;
(2)a与b的乘积的所有可能出现的结果如下表所示:
总共有16种结果,每种结果出现的可能性相同,其中ab=2的结果有2种,
(7分)
∴a与b的乘积等于2的概率是
.
(3)由(2)知:共有16种结果,每种结果出现的可能性相同,其中a、b能使一元二次方程x2+ax-b=0有实数根的结果即a2+4b≥0的情况数有10种,
∴a、b能使一元二次方程x2+ax-b=0有实数根的概率是
=
.
| 1 |
| 2 |
| 1 |
| 2 |
(2)a与b的乘积的所有可能出现的结果如下表所示:
| a b |
1 | 2 | -3 | -4 |
| 1 | 1 | 2 | -3 | -4 |
| 2 | 2 | 4 | -6 | -8 |
| -3 | -3 | -6 | 9 | 12 |
| -4 | -4 | -8 | 12 | 16 |
(7分)
∴a与b的乘积等于2的概率是
| 1 |
| 8 |
(3)由(2)知:共有16种结果,每种结果出现的可能性相同,其中a、b能使一元二次方程x2+ax-b=0有实数根的结果即a2+4b≥0的情况数有10种,
∴a、b能使一元二次方程x2+ax-b=0有实数根的概率是
| 10 |
| 16 |
| 5 |
| 8 |
点评:考查用列树状图的方法解决概率问题;得到所求的情况数是解决本题的关键;用到的知识点为:概率等于所求情况数与总情况数之比.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
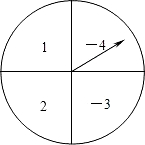 如图所示,有一个可以自由转动的圆形转盘,被平均分成四个扇形,四个扇形内分别标有数字1、2、-3、-4、若将转盘转动两次,每一次停止转动后,指针指向的扇形内的数字分别记为a、b(若指针恰好指在分界线上,则该次不计,重新转动一次,直至指针落在扇形内).
如图所示,有一个可以自由转动的圆形转盘,被平均分成四个扇形,四个扇形内分别标有数字1、2、-3、-4、若将转盘转动两次,每一次停止转动后,指针指向的扇形内的数字分别记为a、b(若指针恰好指在分界线上,则该次不计,重新转动一次,直至指针落在扇形内).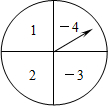 直至指针落在扇形内).
直至指针落在扇形内).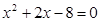 的解的概率.
的解的概率.
