Question

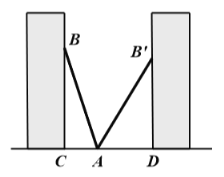
【题目】已知，如图，点，，，在同一条直线上，且，∠A=∠FDE，在①，②∠CBA=∠E，③∠C=∠F中，请选择其中一个条件，证明△ABC≌△DEF．

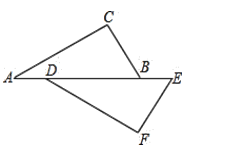
（1）你选择的条件是________（只需填写序号）；

（2）证明．

Answer 1

【答案】(1)见解析；（2）见解析

【解析】

要判定△ABC≌△DEF，已知AD=BE，可证AB=DE，又已知∠A=∠FDE，具备了一组边和一组角对应相等，故可分别选择其中一个条件①AC=DF，②∠CBA=∠E，③∠C=∠F中，分别根据SAS，ASA，AAS证明△ABC≌△DEF．

（1）添加条件①AC=DF．
证明：∵AD=BE，
∴AD+BD=BE+BD，
即AB=DE．
在△ABC和△DEF中，
AB=DE，
∠A=∠FDE，
AC=DF，
∴△ABC≌△DEF（SAS）．

（2）添加条件②∠CBA=∠E．
证明：∵AD=BE，
∴AD+BD=BE+BD，
即AB=DE．
在△ABC和△DEF中，
∠A=∠FDE，
AB=DE，
∠CBA=∠E，
∴△ABC≌△DEF（ASA）．

（3）添加条件③∠C=∠F．
证明：∵AD=BE，
∴AD+BD=BE+BD，
即AB=DE．
在△ABC和△DEF中，
∠A=∠FDE，
∠C=∠F，
AB=DE，
∴△ABC≌△DEF（AAS）．