题目内容
等腰梯形中,上底:腰:下底=1:2:3,则下底角的度数是
- A.30°
- B.45°
- C.60°
- D.90°
C
分析:作两高,构造出直角三角形,运用等腰梯形的性质和三角函数的定义求解.
解答: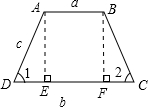 解:作AE⊥CD于E,BF⊥CD于F.
解:作AE⊥CD于E,BF⊥CD于F.
设AB=a,CD=b,AD=c.
根据题意,画出图形.
∵梯形是等腰梯形,
∴∠1=∠2,AD=BC,
∴Rt△ADE≌Rt△BCF,
∴DE=CF,
∴DE=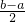 ,
,
∴cos∠1= =
=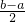 ÷c.
÷c.
∵上底:腰:下底=1:2:3,
∴a:c:b=1:2:3,
∴cos∠1= ,
,
∵∠1<90°,
∴∠1=60°,即底角的度数是60°.
故选C.
点评:本题考查了等腰梯形的性质和特殊角的三角函数值,注意梯形中常做的辅助线:①作高;②平移一腰;③平移对角线;④反向延长两腰.
分析:作两高,构造出直角三角形,运用等腰梯形的性质和三角函数的定义求解.
解答:
 解:作AE⊥CD于E,BF⊥CD于F.
解:作AE⊥CD于E,BF⊥CD于F.设AB=a,CD=b,AD=c.
根据题意,画出图形.
∵梯形是等腰梯形,
∴∠1=∠2,AD=BC,
∴Rt△ADE≌Rt△BCF,
∴DE=CF,
∴DE=
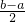 ,
,∴cos∠1=
 =
=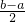 ÷c.
÷c.∵上底:腰:下底=1:2:3,
∴a:c:b=1:2:3,
∴cos∠1=
 ,
,∵∠1<90°,
∴∠1=60°,即底角的度数是60°.
故选C.
点评:本题考查了等腰梯形的性质和特殊角的三角函数值,注意梯形中常做的辅助线:①作高;②平移一腰;③平移对角线;④反向延长两腰.

练习册系列答案
相关题目
等腰梯形中,上底:腰:下底=1:2:3,则下底角的度数是( )
| A、30° | B、45° | C、60° | D、90° |