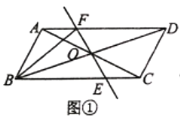
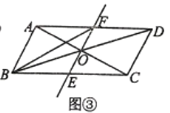
ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌдкОиаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊЖдНЧЯп
ЮЊЖдНЧЯп![]() ЩЯвЛЕуЃЌЧв
ЩЯвЛЕуЃЌЧв![]() ЃЌЙ§
ЃЌЙ§![]() зї
зї![]() ЃЌЗжБ№НЛ
ЃЌЗжБ№НЛ![]() ЁЂ
ЁЂ![]() гк
гк![]() ЁЂ
ЁЂ![]() ЁЃЖЏЕу
ЁЃЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЕФЫйЖШдкЩфЯп
ГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЕФЫйЖШдкЩфЯп![]() ЩЯдЫЖЏЁЃЖЏЕу
ЩЯдЫЖЏЁЃЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЕФЫйЖШдкЯпЖЮ
ГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЕФЫйЖШдкЯпЖЮ![]() ЩЯби
ЩЯби![]()
![]()
![]() ЗНЯђдЫЖЏЁЃвд
ЗНЯђдЫЖЏЁЃвд![]() ЮЊБпзїЕШБп
ЮЊБпзїЕШБп![]() ЁЃвбжЊ
ЁЃвбжЊ![]() ЁЂ
ЁЂ![]() СНЕуЭЌЪБГіЗЂЃЌЕБЕу
СНЕуЭЌЪБГіЗЂЃЌЕБЕу![]() ЗЕЛиЕу
ЗЕЛиЕу![]() ЪБСНЕуЭЌЪБЭЃжЙдЫЖЏЁЃдЫЖЏЪБМфЮЊ
ЪБСНЕуЭЌЪБЭЃжЙдЫЖЏЁЃдЫЖЏЪБМфЮЊ![]() Уы.
Уы.
ЃЈ1ЃЉЧѓЯпЖЮ![]() ЃЌЕБЕу
ЃЌЕБЕу![]() ТфдкЯпЖЮ
ТфдкЯпЖЮ![]() ЩЯЪБ
ЩЯЪБ![]() ЕШгкЖрЩйЃЛ
ЕШгкЖрЩйЃЛ
ЃЈ2ЃЉЩшдЫЖЏЙ§ГЬжа![]() гыОиаЮ
гыОиаЮ![]() ЕФжиЕўВПЗжУцЛ§ЮЊ
ЕФжиЕўВПЗжУцЛ§ЮЊ![]() ЃЌЧыжБНгаДГі
ЃЌЧыжБНгаДГі![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНМАздБфСП
ЕФКЏЪ§ЙиЯЕЪНМАздБфСП![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉНЋЫФБпаЮ![]() ШЦЕу
ШЦЕу![]() а§зЊвЛжмЃЌдкДЫЙ§ГЬжаЃЌЩшжБЯп
а§зЊвЛжмЃЌдкДЫЙ§ГЬжаЃЌЩшжБЯп![]() ЗжБ№гыжБЯп
ЗжБ№гыжБЯп![]() ЁЂ
ЁЂ![]() НЛгкЕу
НЛгкЕу![]() ЁЂ
ЁЂ![]() ЃЌЕБ
ЃЌЕБ![]() ЪЧвд
ЪЧвд![]() ЮЊЕзНЧЕФЕШбќШ§НЧаЮЪБЃЌЧѓ
ЮЊЕзНЧЕФЕШбќШ§НЧаЮЪБЃЌЧѓ![]() ЕФГЄ.
ЕФГЄ.
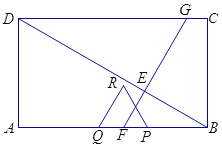
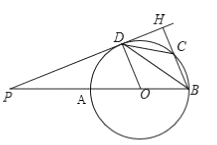
ЁОД№АИЁПЃЈ1ЃЉЯпЖЮBF=4ЃЌЕБЕу![]() ТфдкЯпЖЮ
ТфдкЯпЖЮ![]() ЩЯЪБt=3ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉ
ЩЯЪБt=3ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉ![]() Лђ
Лђ![]() ЃЌ
ЃЌ![]() Лђ
Лђ![]() .
.
ЁОНтЮіЁП
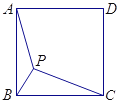
ЃЈ1ЃЉИљОнОиаЮЕФаджЪЃЌНсКЯвбжЊЬѕМўЭЈЙ§НтжБНЧШ§НЧаЮМДПЩЧѓНтЃЛ
ЃЈ2ЃЉЗжЮЊЫФжжЧщПіЃЌЛГіЭМаЮЃЌЧѓГіИїИіШ§НЧаЮЕФУцЛ§ЃЌИљОнЭМаЮМДПЩЕУГіД№АИЃЛ
ЃЈ3ЃЉЯШИљОнНтжБНЧШ§НЧаЮ,ЧѓЕУBFЕФГЄ,дйИљОна§зЊЧѓЕУ![]() ЕФГЄ,зюКѓИљОнЫФБпаЮBCGFа§зЊКѓЕФСНжжВЛЭЌЮЛжУНјааЬжТл,ЧѓЕУDNЕФГЄ.
ЕФГЄ,зюКѓИљОнЫФБпаЮBCGFа§зЊКѓЕФСНжжВЛЭЌЮЛжУНјааЬжТл,ЧѓЕУDNЕФГЄ.
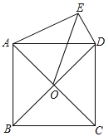
ЃЈ1ЃЉЁпОиаЮABCDжаЃЌAB=9ЃЌAD=![]() ,
,![]()
ЁрЁЯABD=30ЃЌBD=![]() ЃЌ
ЃЌ
ЁпDE=2BEЃЌFGЁЭBDЃЌ
ЁрDE=4![]() ЃЌBE=2
ЃЌBE=2![]()
Ёр![]() ЃЛ
ЃЛ
ЁрЕБЕуRТфдкЯпЖЮCDЪБЃЌІЄPQRЕФИпЮЊ![]() ЃЌдђЕзЮЊ6ЃЌЫљвдt=3.
ЃЌдђЕзЮЊ6ЃЌЫљвдt=3.
ЃЈ2ЃЉЫФжжЧщПіШчЭМЫљЪОЭМ1ЃЌЭМ2,ЭМ3ЃЌЭМ4
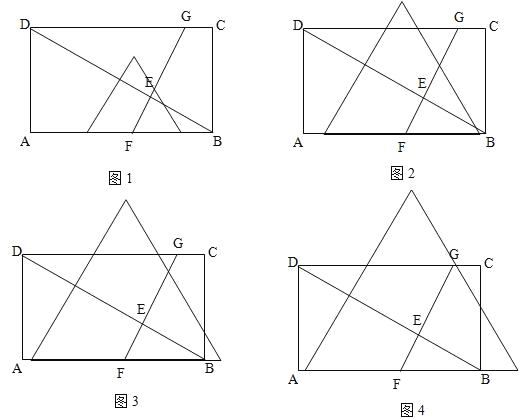
ЭМ1ЫљЪОЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
ЭМ2ЫљЪОЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
ЭМ3 ЫљЪОЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
ЭМ4ЫљЪОЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉгЩЃЈ1ЃЉЕУBF=4ЃЌгЩа§зЊПЩЕУBF'=BF=4ЃЌЁЯF'BC'=ЁЯFBC=90ЁуЃЌЁЯBFG=ЁЯBF'G'=60ЁуЃЌЂйШчЭМ5ЃЌЕБЁїDMNЪЧвдЁЯMDNЃЌЁЯMNDЮЊЕзНЧЕФЕШбќШ§НЧаЮЪБЃЌЁЯN=30ЁуЃЌ
ЁрtanЁЯBNF'=![]() ЃЌ
ЃЌ
Ёр![]() ЃЌМДBN=4
ЃЌМДBN=4![]() ЃЌ
ЃЌ
ЁрDN=BD+BN=6![]() +4
+4![]() =10
=10![]() ЃЛ
ЃЛ
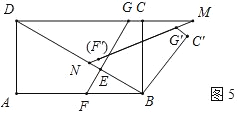
ЂкШчЭМ6ЃЌЕБЁїDMNЪЧвдЁЯMDNЃЎЁЯNMDЮЊЕзНЧЕФЕШбќШ§НЧаЮЪБЃЌЁЯBNM=60Ёу=ЁЯBF'MЃЌДЫЪБЃЌF'гыNжиКЯЃЌЙЪBF'=BN=4ЃЌ
ЁрDN=BDЉBN=6![]() Љ4ЃЎ
Љ4ЃЎ
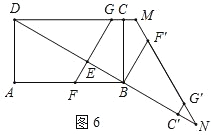
ЙЪД№АИЮЊЃК10![]() Лђ6
Лђ6![]() Љ4
Љ4

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИЁОЬтФПЁПФГаЃбЇЩњЛсзМБИЕїВщСљФъМЖбЇЩњВЮМгЁАЮфЪѕРрЁБЁЂЁАЪщЛРрЁБЁЂЁАЦхХЦРрЁБЁЂЁАЦїРжРрЁБЫФРраЃБОПЮГЬЕФШЫЪ§ЃЎ
ЃЈ1ЃЉШЗЖЈЕїВщЗНЪНЪБЃЌМзЭЌбЇЫЕЃКЁАЮвЕНСљФъМЖЃЈ1ЃЉАрШЅЕїВщШЋЬхЭЌбЇЁБЃЛввЭЌбЇЫЕЃКЁАЗХбЇЪБЮвЕНаЃУХПкЫцЛњЕїВщВПЗжЭЌбЇЁБЃЛБћЭЌбЇЫЕЃКЁАЮвЕНСљФъМЖУПИіАрЫцЛњЕїВщвЛЖЈЪ§СПЕФЭЌбЇЁБЃЎЧыжИГіФФЮЛЭЌбЇЕФЕїВщЗНЪНзюКЯРэЃЎ
РрБ№ | ЦЕЪ§ЃЈШЫЪ§ЃЉ | ЦЕТЪ |
ЮфЪѕРр | 0.25 | |
ЪщЛРр | 20 | 0.20 |
ЦхХЦРр | 15 | b |
ЦїРжРр | ||
КЯМЦ | a | 1.00 |
ЃЈ2ЃЉЫћУЧВЩгУСЫзюЮЊКЯРэЕФЕїВщЗНЗЈЪеМЏЪ§ОнЃЌВЂЛцжЦСЫШчЭМЫљЪОЕФЭГМЦБэКЭЩШаЮЭГМЦЭМЃЎ
ЧыФуИљОнвдЩЯЭМБэЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
Ђйa=_____ЃЌb=_____ЃЛ
ЂкдкЩШаЮЭГМЦЭМжаЃЌЦїРжРрЫљЖдгІЩШаЮЕФдВаФНЧЕФЖШЪ§ЪЧ_____ЃЛ
ЂлШєИУаЃСљФъМЖгабЇЩњ560ШЫЃЌЧыФуЙРМЦДѓдМгаЖрЩйбЇЩњВЮМгЮфЪѕРраЃБОПЮГЬЃЎ