题目内容
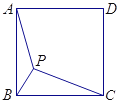
【题目】如图,点![]() 在边长为2的正方形
在边长为2的正方形![]() 内,连结
内,连结![]() 、
、![]() 、
、![]() ,则
,则![]() 的最小值为________.
的最小值为________.
【答案】![]()
【解析】
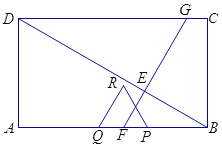
△BPC绕B点顺时针旋转60度,可得△PBE为等边三角形,若PA+PB+PC=AP+PE+EF要使最小只要AP,PE,EF在一条直线上,求出AF的值即可.
△BPC绕B点顺时针旋转60度,可得△PBE为等边三角形.
即得PA+PB+PC=AP+PE+EF要使最小只要AP,PE,EF在一条直线上,
即如下图:可得最小PA+PB+PC=AF.

此时∠EBC+∠CBP=∠FBE+∠EBC=60°=∠FBC,
所以∠ABF=90°+60°=150°,
∠MBF=30°,
BM=![]() ,MF=1,
,MF=1,
则AM=2+![]() ,
,
在△AMF中,勾股定理得:
AM2+MF2=AF2
AF=![]() .
.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目