题目内容
如图,l1∥l2,l3与l1、l2相交于C、D二点,点P在l3上,在图(1)、(2)、(3)中分别探究∠PAC、∠APB、∠PBD三者间关系,并证明.
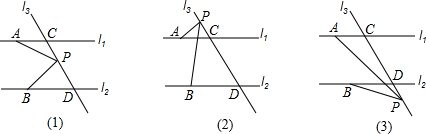
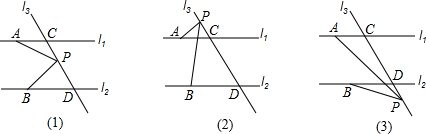
分析:(1)首先过点P作PE∥l1,由l1∥l2,可得PE∥l1∥l2,即可证得∠1=∠PAC,∠2=∠PBD,继而证得:∠APB=∠PAC+∠PBD.
(2)由l1∥l2,根据平行线与三角形外角的性质,即可证得∠PAC+∠APB=∠PBD.
(3)由l1∥l2,根据平行线与三角形外角的性质,即可证得∠PBD+∠APB=∠PAC.
(2)由l1∥l2,根据平行线与三角形外角的性质,即可证得∠PAC+∠APB=∠PBD.
(3)由l1∥l2,根据平行线与三角形外角的性质,即可证得∠PBD+∠APB=∠PAC.
解答: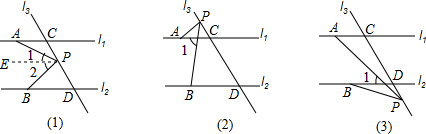 (1)∠APB=∠PAC+∠PBD.
(1)∠APB=∠PAC+∠PBD.
证明:过点P作PE∥l1,
∵l1∥l2,
∴PE∥l1∥l2,
∴∠1=∠PAC,∠2=∠PBD,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
(2)∠PAC+∠APB=∠PBD.
证明:∵l1∥l2,
∴∠1=∠PBD,
∵∠1=∠PAC+∠APB,
∴∠PAC+∠APB=∠PBD.
(3)∠PBD+∠APB=∠PAC.
证明:∵l1∥l2,
∴∠1=∠PAC,
∵∠1=∠PBD+∠APB,
∴∠PBD+∠APB=∠PAC.
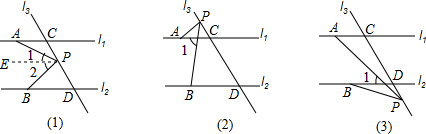 (1)∠APB=∠PAC+∠PBD.
(1)∠APB=∠PAC+∠PBD.证明:过点P作PE∥l1,
∵l1∥l2,
∴PE∥l1∥l2,
∴∠1=∠PAC,∠2=∠PBD,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
(2)∠PAC+∠APB=∠PBD.
证明:∵l1∥l2,
∴∠1=∠PBD,
∵∠1=∠PAC+∠APB,
∴∠PAC+∠APB=∠PBD.
(3)∠PBD+∠APB=∠PAC.
证明:∵l1∥l2,
∴∠1=∠PAC,
∵∠1=∠PBD+∠APB,
∴∠PBD+∠APB=∠PAC.
点评:此题考查了平行线的性质与三角形外角的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
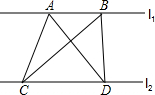 如图,l1∥l2,A、B为直线l1上两点,C、D为直线l2上两点,则△ACD与△BCD的面积大小关系是( )
如图,l1∥l2,A、B为直线l1上两点,C、D为直线l2上两点,则△ACD与△BCD的面积大小关系是( )| A、S△ACD<S△BCD | B、S△ACD=S△BCD | C、S△ACD>S△BCD | D、不能确定 |
 13、如图,l1∥l2,∠1=120°,∠2=100°,则∠3=( )
13、如图,l1∥l2,∠1=120°,∠2=100°,则∠3=( )
 如图,l1∥l2,AB⊥AC,∠ABC=50°,则∠1=( )度.
如图,l1∥l2,AB⊥AC,∠ABC=50°,则∠1=( )度. 如图,l1∥l2∥l3,已知L1与l3之间的距离为8cm,l1与l2之间的距离为3cm,则l2与l3之间的距离为
如图,l1∥l2∥l3,已知L1与l3之间的距离为8cm,l1与l2之间的距离为3cm,则l2与l3之间的距离为