题目内容
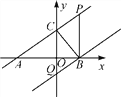
【题目】如图,若直线y=![]() x+2分别交x轴、y轴于A,C两点,点P是该直线上在第一象限内的一点,PB⊥x轴,B为垂足,且S△ABC=6.
x+2分别交x轴、y轴于A,C两点,点P是该直线上在第一象限内的一点,PB⊥x轴,B为垂足,且S△ABC=6.
(1)求点B和点P的坐标;
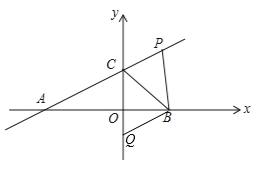
(2)过点B作直线BQ∥AP,交y轴于点Q,求点Q的坐标和四边形BPCQ的面积.
【答案】(1)B(2,0),P(2,3);(2)6.
【解析】试题分析:(1)利用一次函数图象上点的坐标特征可求出点A、C的坐标,根据S△ABC=6可求出点B的坐标,再利用一次函数图象上点的坐标特征可求出点P的坐标;
(2)由PB⊥x轴可得出PB∥CQ,结合BQ∥AP可得出四边形BPCQ为平行四边形,再根据点B、C、P的坐标即可得出点Q的坐标以及四边形BPCQ的面积.
试题解析:解:(1)当x=0时,y=![]() x+2=2,∴点C的坐标为(0,2);
x+2=2,∴点C的坐标为(0,2);
当y=![]() x+2=0时,x=﹣4,∴点A的坐标为(﹣4,0).
x+2=0时,x=﹣4,∴点A的坐标为(﹣4,0).
设点B的坐标为(m,0),则S△ABC=![]() ABOC=
ABOC=![]() ×[m﹣(﹣4)]×2=6,解得:m=2,点B的坐标为(2,0).当x=2时,y=
×[m﹣(﹣4)]×2=6,解得:m=2,点B的坐标为(2,0).当x=2时,y=![]() x+2=3,∴点P的坐标为(2,3).
x+2=3,∴点P的坐标为(2,3).
(2)∵PB⊥x轴,∴PB∥CQ.∵BQ∥AP,∴四边形BPCQ为平行四边形.∵点C(0,2),点B(2,0),点P(2,3),∴点Q的坐标为(0,﹣1),∴S平行四边形BPCQ=OBBP=2×3=6.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目