ЬтФПФкШн
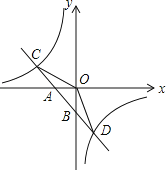
ЁОЬтФПЁПШчЭМЃЌжБЯпlЃКy=Љ3x+3гыxжсЁЂyжсЗжБ№ЯрНЛгкAЁЂBСНЕуЃЌХзЮяЯпy=ax2Љ2ax+a+4ЃЈaЃМ0ЃЉОЙ§ЕуBЃЎ

ЃЈ1ЃЉЧѓaЕФжЕЃЌВЂаДГіХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉвбжЊЕуMЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌВЂЧвЕуMдкЕквЛЯѓЯоФкЃЌСЌНгAMЁЂBMЃЌ
ЂйЕБЕуMЃЈ2ЃЌnЃЉЪБЃЌЧѓnЃЌВЂЧѓЁїABMЕФУцЛ§.
ЂкЕБЕуMЕФКсзјБъЮЊmЃЌЁїABMЕФУцЛ§ЮЊSЃЌЧѓSгыmЕФКЏЪ§БэДяЪНЃЌВЂЧѓГіSЕФзюДѓжЕКЭДЫЪБЕуMЕФзјБъ.
ЁОД№АИЁПЃЈ1ЃЉa=Љ1ЃЌy=Љx2+2x+3ЃЛ
ЃЈ2ЃЉЂйn=3ЃЌSЁїABM=3ЃЛ
ЂкS =Љ![]() ЃЈmЉ
ЃЈmЉ![]() ЃЉ2+
ЃЉ2+![]() ЃЌMЁфЕФзјБъЮЊЃЈ
ЃЌMЁфЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌ SШЁЕУзюДѓжЕ
ЃЉЃЌ SШЁЕУзюДѓжЕ![]() ЃЎ
ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉСювЛДЮКЏЪ§x=0ЃЌЕУГіBЕФзјБъЃЌНЋBЕФзјБъДњШыЖўДЮКЏЪ§НтЮіЪНМДПЩНтГіaЃЛЃЈ2ЃЉЂйСювЛДЮКЏЪ§y=0ЃЌЕУГіA ЕФзјБъЃЌСюЖўДЮКЏЪ§x=2ЃЌПЩЕУnМАMЕФзјБъЃЌИљОнAЁЂBЁЂMЕФзјБъПЩЧѓГіЁїABMЕФУцЛ§ЃЛЂквЊБэЪОГіЁїABMЕФУцЛ§ПЩгУИюВЙЗЈЃЌSЪЧЙигкmЕФЖўДЮКЏЪ§ЃЌвЊЧѓзюжЕЃЌНЋЖўДЮКЏЪ§НтЮіЪНаДГЩЖЅЕуЪНМДПЩ.
ЪдЬтНтЮіЃК
НтЃКЃЈ1ЃЉАбx=0ДњШыy=Ѓ3x+3ЕУy=3ЃЌ
ЁрBЃЈ0ЃЌ3ЃЉЃЌ
АбBЃЈ0ЃЌ3ЃЉДњШыy=ax2Ѓ2ax+a+4ЃЌ
Ёр3=a+4ЃЌ
Ёрa=Ѓ1ЃЌ
Ёрy=Ѓx2+2x+3ЃЛ
ЃЈ2ЃЉ Сюy=0ЕУЃК0=Ѓx2+2x+3ЃЌ
Ёрx=Ѓ1Лђ3ЃЌ
ЁрХзЮяЯпгыxжсЕФНЛЕуКсзјБъЮЊЃ1КЭ3ЃЌ
ЁпMдкХзЮяЯпЩЯЃЌЧвдкЕквЛЯѓЯоФкЃЌ
Ёр0ЃМmЃМ3ЃЌ
Сюy=0ДњШыy=Ѓ3x+3ЃЌ
Ёрx=1ЃЌ
ЁрAЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЌ
ЕБx=2ЪБЃЌДњШыy=Ѓx2+2x+3=3ЃЌдђMЃЈ2ЃЌ3ЃЉМДn=3ЃЌ
ДЫЪБMB//xжсЃЌMB=2ЃЌ SЁїABM=2ЁС3ЁС![]() =3ЃЛ
=3ЃЛ
ЃЈ3ЃЉ

ШчЭМЃЌСЌНгOM,
Сюx=mЃЌy=Ѓm2+2m+3ЃЌ
ЁрMЕФзјБъЮЊЃЈmЃЌЃm2+2m+3ЃЉЃЌ
S=SЫФБпаЮOAMBЉSЁїAOB
=SЁїOBM+SЁїOAMЉSЁїAOB
=![]() ЁСmЁС3+
ЁСmЁС3+![]() ЁС1ЁСЃЈЃm2+2m+3ЃЉЃ
ЁС1ЁСЃЈЃm2+2m+3ЃЉЃ![]() ЁС1ЁС3
ЁС1ЁС3
=Ѓ![]() m2+
m2+![]() mЃЌ
mЃЌ
ЁпS =Ѓ![]() ЃЈmЃ
ЃЈmЃ![]() ЃЉ2+
ЃЉ2+![]() ЃЌ
ЃЌ
ЁрЕБm=![]() ЪБЃЌSШЁЕУзюДѓжЕ
ЪБЃЌSШЁЕУзюДѓжЕ![]() ЃЎ
ЃЎ
ЕБm=![]() ЪБЃЌy=ЃЃЈ
ЪБЃЌy=ЃЃЈ![]() ЃЉ2+2ЁС
ЃЉ2+2ЁС![]() +3=
+3=![]() ЃЌ
ЃЌ
ЁрMЁфЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉ.
ЃЉ.