题目内容
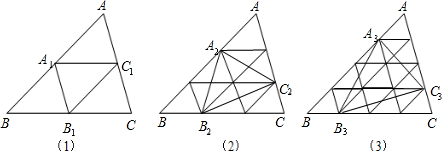
如图，已知△ABC的面积S△ABC=1．
在图（1）中，若
=
=
=
，则S△A1B1C1=
；
在图（2）中，若
=
=
=
，则S△A2B2C2=
；
在图（3）中，若
=
=
=
，则S△A3B3C3=
；
按此规律，若
=
=
=
，则S△A7B7C7=
（提示：用三点式求出抛物线的解析式，再求函数值）
（提示：用三点式求出抛物线的解析式，再求函数值）．
在图（1）中，若
| AA1 |
| AB |
| BB1 |
| BC |
| CC1 |
| CA |
| 1 |
| 2 |
| 1 |
| 4 |
在图（2）中，若
| AA2 |
| AB |
| BB2 |
| BC |
| CC2 |
| CA |
| 1 |
| 3 |
| 1 |
| 3 |
在图（3）中，若
| AA3 |
| AB |
| BB3 |
| BC |
| CC3 |
| CA |
| 1 |
| 4 |
| 7 |
| 16 |
按此规律，若
| AA7 |
| AB |
| BB7 |
| BC |
| CC7 |
| CA |
| 1 |
| 8 |
| 43 |
| 64 |
| 43 |
| 64 |
分析：求得三角形ABC的面积S与对应边的比值之间的函数关系，然后代入比值求函数值即可．
解答：解：设函数关系为S=ax2+bx+c，
∵若
=
=
=
，则S△A1B1C1=
；
若
=
=
=
，则S△A2B2C2=
；
若
=
=
=
，则S△A3B3C3=
；
∴
解得：a=3，b=-3，c=1
∴S=3x2-3x+1
∴若
=
=
=
，S=3×（
）2+（-3）×
+1=
．
故答案为
．
∵若
| AA1 |
| AB |
| BB1 |
| BC |
| CC1 |
| CA |
| 1 |
| 2 |
| 1 |
| 4 |
若
| AA2 |
| AB |
| BB2 |
| BC |
| CC2 |
| CA |
| 1 |
| 3 |
| 1 |
| 3 |
若
| AA3 |
| AB |
| BB3 |
| BC |
| CC3 |
| CA |
| 1 |
| 4 |
| 7 |
| 16 |
∴
|
解得：a=3，b=-3，c=1
∴S=3x2-3x+1
∴若
| AA7 |
| AB |
| BB7 |
| BC |
| CC7 |
| CA |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 43 |
| 64 |
故答案为
| 43 |
| 64 |
点评：主要考查了学生通过特例分析从而归纳总结出一般结论的能力．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．
练习册系列答案
相关题目
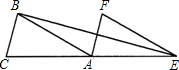如图，已知△ABC的面积为4，且AB=AC，现将△ABC沿CA方向平移CA的长度，得到△EFA．
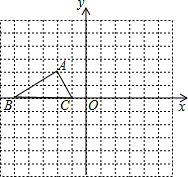（2010•孝感模拟）如图，已知△ABC的三个顶点的坐标分别为A（-2，2）、B（-5，0）、C（-1，0）．
如图，已知△ABC的三个顶点的坐标分别是A（-7，1），B（-3，3），C（-2，6）．