题目内容
 27、已知:如图,在⊙O中,OA是半径,CD是弦,OA交CD于点E.现有四个条件:①∠COA=∠AOD=60°;②AC=AD=OA;③点E分别是AO、CD的中点;④OA⊥CD.
27、已知:如图,在⊙O中,OA是半径,CD是弦,OA交CD于点E.现有四个条件:①∠COA=∠AOD=60°;②AC=AD=OA;③点E分别是AO、CD的中点;④OA⊥CD.(1)其中能推出四边形OCAD是菱形的条件有
①②③
(填写序号);(2)选择(1)中你所写的一个条件,说明其结论的正确性.
分析:根据菱形的判定判断.
解答:解:(1)①②③;
①由∠COA=∠AOD=60°,可得,CA=AD,△AOC和△AOD是等边三角形,所以OCAD得四边相等,则能推出是菱形;
②由AC=AD=OA,可得AC=AD=OC=OD,则能推出是菱形;
③点E分别是AO、CD的中点,根据垂径定理可得OA⊥CD,则能推出是菱形.
④而OA⊥CD,只能得出CE=DE,不能得出OE=AE,故不能推出.
(2)任选一种证明即可,如②:
∵AC=AD=OA,OA=OC=OD
∴AC=AD=OC=OD,
∴四边形OCAD是菱形.
①由∠COA=∠AOD=60°,可得,CA=AD,△AOC和△AOD是等边三角形,所以OCAD得四边相等,则能推出是菱形;
②由AC=AD=OA,可得AC=AD=OC=OD,则能推出是菱形;
③点E分别是AO、CD的中点,根据垂径定理可得OA⊥CD,则能推出是菱形.
④而OA⊥CD,只能得出CE=DE,不能得出OE=AE,故不能推出.
(2)任选一种证明即可,如②:
∵AC=AD=OA,OA=OC=OD
∴AC=AD=OC=OD,
∴四边形OCAD是菱形.
点评:菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义,②四边相等,③对角线互相垂直平分.

练习册系列答案
相关题目
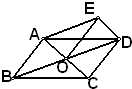 24、已知:如图,在?ABCD中,对角线AC交BD于点O,四边形AODE是平行四边形.求证:四边形ABOE、四边形DCOE都是平行四边形.
24、已知:如图,在?ABCD中,对角线AC交BD于点O,四边形AODE是平行四边形.求证:四边形ABOE、四边形DCOE都是平行四边形.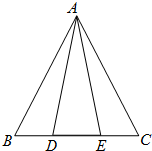 21、已知:如图,在△ABC中,AB=AC,点D,E在边BC上,且BD=CE.
21、已知:如图,在△ABC中,AB=AC,点D,E在边BC上,且BD=CE.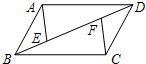 (1)计算:
(1)计算: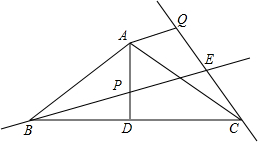 点A重合.将线段AP绕点A逆时针旋转到AQ,使∠PAQ=∠BAC,连接BP,CQ
点A重合.将线段AP绕点A逆时针旋转到AQ,使∠PAQ=∠BAC,连接BP,CQ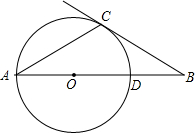 (2012•密云县一模)已知:如图,在△ABC中,∠A=∠B=30°,D是AB 边上一点,以AD为直径作⊙O恰过点C.
(2012•密云县一模)已知:如图,在△ABC中,∠A=∠B=30°,D是AB 边上一点,以AD为直径作⊙O恰过点C.