Question

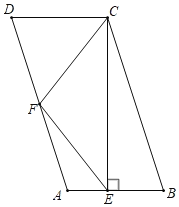
【题目】如图，在四边形ABCD中，AD∥BC，AD=BC=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF．

（1）若∠ADC=80°，求∠ECF；

（2）求证：∠ECF=∠CEF．

Answer 1

【答案】（1）∠ECF=40°；（2）证明见解析．

【解析】

（1）根据AD∥BC，AD=BC=2AB，可证得四边形ABCD是平行四边形，根据F是AD的中点，可得AF=FD=CD，根据三角形内角和定理求得∠DFC=∠DCF=（180°﹣80°）=50°，根据CE⊥AB，可得∠DCE=90°，继而求解；

（2）延长EF，交CD延长线于M，易知∠A=∠MDF，求证△AEF≌△DMF，继而可得FE=MF，∠AEF=∠M，再根据CE⊥AB，求得∠AEC=∠ECD=90°，根据等腰直角三角形性质可知，FC=EM=FE，进而求证结论．

（1）∵AD∥BC，AD=BC，

∴四边形ABCD是平行四边形．

∵F是AD的中点，

∴AF=FD．

∵在ABCD中，AD=2AB，

∴AF=FD=CD，

∴∠DFC=∠DCF=（180°﹣80°）=50°．

∵CE⊥AB，

∴CE⊥CD，

∴∠DCE=90°，

∴∠ECF=90°－50°＝40°；

（2）如图，延长EF，交CD延长线于M．

∵四边形ABCD是平行四边形，

∴AB∥CD，

∴∠A=∠MDF．

∵F为AD中点，

∴AF=FD，

在△AEF和△DFM中，，

∴△AEF≌△DMF（ASA），

∴FE=MF，∠AEF=∠M．

∵CE⊥AB，

∴∠AEC=90°，

∴∠AEC=∠ECD=90°，

∵FM=EF，

∴FC=EM=FE，

∴∠ECF=∠CEF．