题目内容
如图,经过原点的抛物线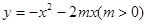 与
与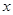 轴的另一个交点为A.过点
轴的另一个交点为A.过点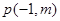 作直线
作直线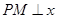 轴于点M,交抛物线于点B,过点B作直线BC∥
轴于点M,交抛物线于点B,过点B作直线BC∥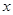 轴与抛物线交于点C(B、C不重合),连结CP.
轴与抛物线交于点C(B、C不重合),连结CP.
(1)当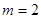 时,求点A的坐标及BC的长;
时,求点A的坐标及BC的长;
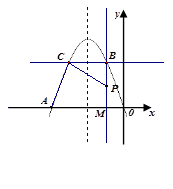
(2)当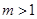 时,连结CA,问
时,连结CA,问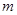 为何值时
为何值时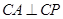 ?
?
(3)过点P作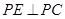 且
且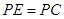 ,问是否存在
,问是否存在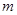 ,使得点E落在坐标轴上?若存在,求出所有满足要求的
,使得点E落在坐标轴上?若存在,求出所有满足要求的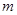 的值,并求出相对应的点E坐标;若不存在,请说明理由.
的值,并求出相对应的点E坐标;若不存在,请说明理由.
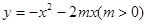 与
与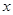 轴的另一个交点为A.过点
轴的另一个交点为A.过点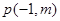 作直线
作直线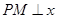 轴于点M,交抛物线于点B,过点B作直线BC∥
轴于点M,交抛物线于点B,过点B作直线BC∥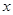 轴与抛物线交于点C(B、C不重合),连结CP.
轴与抛物线交于点C(B、C不重合),连结CP.
(1)当
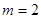 时,求点A的坐标及BC的长;
时,求点A的坐标及BC的长;(2)当
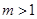 时,连结CA,问
时,连结CA,问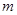 为何值时
为何值时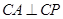 ?
?(3)过点P作
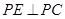 且
且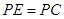 ,问是否存在
,问是否存在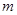 ,使得点E落在坐标轴上?若存在,求出所有满足要求的
,使得点E落在坐标轴上?若存在,求出所有满足要求的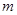 的值,并求出相对应的点E坐标;若不存在,请说明理由.
的值,并求出相对应的点E坐标;若不存在,请说明理由.(1)A(-4,0) ,BC="2" (2)m=2时 (3)存在
试题分析:解:(1)当m=2时,
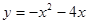 ,
,令y=0,得
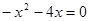 ,∴
,∴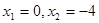
∴A(-4,0)
当x=-1时,y=3,∴B(-1,3)
∵抛物线
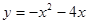 的对称轴为直线x=-2,
的对称轴为直线x=-2,又∵B,C关于对称轴对称,∴BC=2.
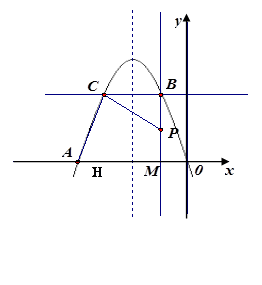
(2)过点C作CH⊥x轴于点H(如图),
由已知得∠ACP=∠BCH=90°,
∴∠ACH=∠PCB
又∵∠AHC=∠PBC=90°,
∴△ACH∽△PCB,
∴
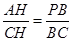 .
.∵抛物线
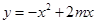 的对称轴为直线x=-m,其中m>1,
的对称轴为直线x=-m,其中m>1,又∵B,C关于对称轴对称,
∴
 ,
,∵
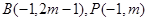
∴
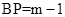
又∵

∴
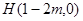 ,
,∴
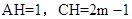
∴
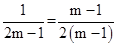 ∴
∴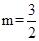 .
.(3)∵B,C不重合,∴m≠1.(I)当m>1时,BC=2(m-1),PM=m, BP=m-1.
(i)若点E在x轴上(如图1),
∵∠CPE=90°,∴∠MPE+∠BPC=∠MPE+∠MEP=90°,
∴∠BPC=∠MEP. 又∵∠CPB=∠PME=90°,PC=EP
∴△BPC≌△MEP,∴BC=PM,
∴2(m-1)=m,
∴m=2,此时点E的坐标是(-2,0).
(II)当0<m<1时,BC=2(1-m),PM=m, BP=1-m,
(i)若点E在x轴上, 易证△BPC≌△MEP,∴BC=PM,
∴2(1-m)=m,∴
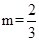 ,此时点E的坐标是
,此时点E的坐标是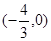 .
.(ii)若点E在y轴上,
过点P作PN⊥y轴于点N,易证△BPC≌△NPE,∴BP=NP=OM=1,
∴1-m=1,∴m=0(舍去).
综上所述,当m=2时,点E的坐标是(-2,0)或(0,4);当
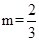 时,点E的坐标是
时,点E的坐标是 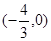 .
.点评:难度系数较大,考生应熟练掌握抛物线的基本性质,包括对称轴的公式,抛物线的顶点等,相似三角形的判定,全等三角形的判定等等,综合知识,数形结合。

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
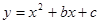 的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是 ( )
的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是 ( )
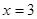
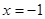
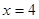
 ,
, 分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有
分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有 ,经过点A、B、C的抛物线的对称轴与直线
,经过点A、B、C的抛物线的对称轴与直线
 绕点C顺时针旋转一个锐角时,它与抛物线的另一个交点为P(x,y),求四边形APCB面积S关于x的函数解析式,并求S的最大值;
绕点C顺时针旋转一个锐角时,它与抛物线的另一个交点为P(x,y),求四边形APCB面积S关于x的函数解析式,并求S的最大值;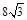 米.请你建立适当的平面直角坐标系解决下列问题.
米.请你建立适当的平面直角坐标系解决下列问题. 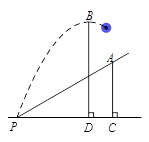
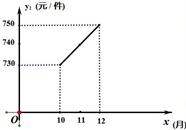
 的图象可能是( )
的图象可能是( )


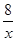

 (
(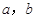 为常数)的图象如下,则
为常数)的图象如下,则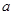 的值为( )
的值为( )


