题目内容
【题目】如图,AB是⊙O的直径,点C在⊙O上,过点C的切线交AB的延长线于点D,∠ACD=120°.
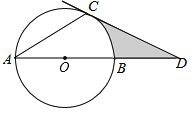
(1)求证:AC=CD;
(2)若⊙O的半径为2,求图中阴影部分的面积.
【答案】(1)证明见解析;(2)S阴影=![]() .
.
【解析】
(1)连接OC,则有∠OCD=90°,由已知从而可得∠A的度数,由内角和从而可得∠D的度数,从而得证;
(2)用△OCD的面积减去扇形OCB的面积即可得到阴影部分的面积.
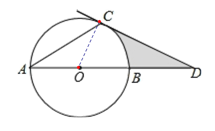
(1)连接OC,∵OC是切线,∴∠OCD=90°,∵∠ACD=120°,∴∠ACO=∠ACD-∠OCD=30°,∵OA=OC,∴∠A=∠ACO=30°,∴∠D=180°-∠A-∠ACD=30°=∠A,∴AC=CD;
(2)由(1)可得∠COD=60°,∠OCD=90°,∴OD=2OC=4,CD=2![]() ,
,
∴S阴影=S△OCD-S扇形OCB=![]() ×2×2
×2×2![]() -
-![]() =
=![]()

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目