题目内容
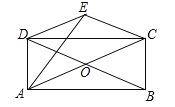
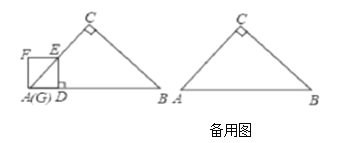
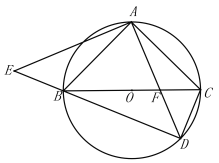
【题目】如图，在△ABC中，
，BC为
的直径，D为任意一点，连接AD交BC于点F，EA⊥AD交DB的延长线于E，连接CD．
（1）求证：△ABE≌△ACD；
（2）填空：①当∠CAD的度数为 时，四边形ABDC是正方形；
②若四边形ABDC的面积为4，则AD的长为 ．
【答案】（1）见解析；（2）①45°；②
【解析】
（1）利用已知条件可证明
，
，又因为
，即可证明结论；
（2）①四边形ABDC是正方形，则
，又因为
，因此，可推出
；②利用面积可求出正方形ABCD的边长为2，利用勾股定理即可求出AD的长．
解：（1）证明∵BC为
直径
∴
∴
又
∴
又
∴
又
∴△ABE≌△ACD．
（2）①∵四边形ABDC是正方形，
∴
∵，BC为的直径
∴
∴
故答案为：45°；
②∵四边形ABDC的面积为4
∴
∵
∴
故答案为：．
练习册系列答案
相关题目
