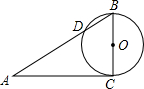
题目内容
如图,AB是⊙O的直径,AB=4,过点B作⊙O的切线,C是切线上一点,且BC=2,P是线段OA中点,连接PC交⊙O于点D,过点P作PC的垂线,交切线BC于点E,交⊙O于点F,连接DF交AB于点G,则PE的长为______.


∵AB是⊙O的直径,AB=4,
∴OA=OB=
AB=2,
∵P是线段OA中点,
∴OP=
OA=1,
∴BP=OB+OP=3,
∵CE是⊙O的切线,
∴AB⊥CE,
∵BC=2,
在Rt△BCP中,BP=
=
,
∵CP⊥EP,
∴∠BCP+∠BPE=90°,
∵∠E+∠BPE=90°,
∴∠BCP=∠E,
∵∠PBC=∠EBP=90°,
∴△PBC∽△EBP,
∴BC:BP=PC:PE,
∴PE=
=
.
故答案为:
.
∴OA=OB=
| 1 |
| 2 |
∵P是线段OA中点,
∴OP=
| 1 |
| 2 |
∴BP=OB+OP=3,
∵CE是⊙O的切线,
∴AB⊥CE,
∵BC=2,
在Rt△BCP中,BP=
| BC2+BP2 |
| 13 |
∵CP⊥EP,
∴∠BCP+∠BPE=90°,
∵∠E+∠BPE=90°,
∴∠BCP=∠E,
∵∠PBC=∠EBP=90°,
∴△PBC∽△EBP,
∴BC:BP=PC:PE,
∴PE=
| BP•PC |
| BC |
3
| ||
| 2 |
故答案为:
3
| ||
| 2 |

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目