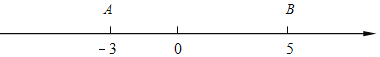��Ŀ����
����Ŀ��ֱ��y����x+6��x�ύ��A����y�ύ��B��ֱ��CD��y�ύ��C��0��2����ֱ��AB����D����D��DE��x����E��2��0����
��1����ֱ��CD�ĺ�������ʽ��
��2��P��x����һ���㣬��P��x��Ĵ��ߣ��ֱ���ֱ��AB��CD����M��N����MN�ij�Ϊd��P��ĺ�����Ϊt�����d��t֮��ĺ�����ϵʽ��
��3���ڣ�2���������£���tΪ��ֵʱ����M��N��E��DΪ������ı�����ƽ���ı��Σ���ֱ��д�������
���𰸡���1��ֱ��CD�ĺ�������ʽΪy��x+2����2����t��2ʱ��d����2t+4����t��2ʱ��d��2t��4����3����t��ֵΪ0��4ʱ����M��N��E��DΪ������ı�����ƽ���ı��Σ�
��������
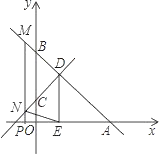
��1���������������D�����꣬�����ô���ϵ���������ֱ��CD�ĺ�������ʽ��
��2����t�ɷֱ��ʾ��M��N�����꣬��ɱ�ʾ��S��t֮��Ĺ�ϵʽ��
��3����������֪MN��DE������ƽ���ı��ε����ʿ�֪MN��DE���ɣ�2���Ĺ�ϵʽ�ɵõ�����t�ķ��̣������t��ֵ��
��1��ֱ��CD��y���ཻ��C��
����ֱ��CD����ʽΪy��kx+2����x��2�����пɵ�y��4��
��D��2��4����
��D����������пɵã�2k+2��4��
��k��1��ֱ��CD�ĺ�������ʽΪy��x+2��
��2�������������֪����OA��t��
��x��t����y����x+6�пɵ�y����t+6
��M��t����t+6����
��x��t����y��x+2�пɵ�y��t+2��
��N��t��t+2����
��t��2ʱ��d����t+6����t+2������2t+4����
��t��2ʱ��d��t+2������t+6����2t��4��
��3���������֪MN��DE��
����M��N��E��DΪ������ı�����ƽ���ı��Σ�
��MN��DE��4��
��|2t��4|��4�����t��0��t��4��
����t��ֵΪ0��4ʱ����M��N��E��DΪ������ı�����ƽ���ı��Σ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�