题目内容
 如图,△ABC的三边分别为AC=5,BC=12,AB=13,将△ABC沿AD折叠,使AC落在AB上.
如图,△ABC的三边分别为AC=5,BC=12,AB=13,将△ABC沿AD折叠,使AC落在AB上.
(1)试判断△ABC的形状,并说明理由;
(2)求折痕AD的长.
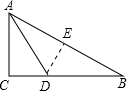 解:(1)△ABC是直角三角形;
解:(1)△ABC是直角三角形;∵AC2+BC2=52+122=169=AB2,
∴∠C=90°;
∴△ABC是直角三角形.
(2)设折叠后点C与AB上的点E重合.
设CD=x,则DE=x,AE=5,BE=8,BD=12-x;
∵∠AED=∠C=90°,
∴在Rt△EBD中,x2+82=(12-x)2,
解得:x=
 ,
,∴AD=
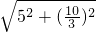 =
=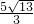 .
.分析:(1)根据勾股定理的逆定理,判断AC2+BC2=52+122=AB2是否成立即可.
(2)设折叠后点C与AB上的点E重合.在Rt△EBD中,根据勾股定理即可得到一个关于DE的方程,解方程即可求解.
点评:本题主要考查了勾股定理的逆定理,以及利用勾股定理把求线段的长的问题转化为方程问题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
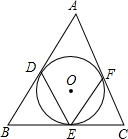 如图,△ABC的三边分别切⊙O于D,E,F,若∠A=40°,则∠DEF=
如图,△ABC的三边分别切⊙O于D,E,F,若∠A=40°,则∠DEF=
 如图,△ABC的三边AB、BC、AC的长分别为4,6,8,其三条角平分线将△ABC分成三个三角形,则S△OAB:S△OBC:S△OAC=
如图,△ABC的三边AB、BC、AC的长分别为4,6,8,其三条角平分线将△ABC分成三个三角形,则S△OAB:S△OBC:S△OAC= 如图,△ABC的三边长分别为AC=12,AB=15,BC=9.若将△ABC沿线段AD折叠,点C正好落在AB边上的点E处.求线段CD的长度.
如图,△ABC的三边长分别为AC=12,AB=15,BC=9.若将△ABC沿线段AD折叠,点C正好落在AB边上的点E处.求线段CD的长度. 如图,△ABC的三边长分别是6cm、8cm、10cm,现在分别取三边的中点E、F、G,顺次连接E、F、G,则△EFG的面积为
如图,△ABC的三边长分别是6cm、8cm、10cm,现在分别取三边的中点E、F、G,顺次连接E、F、G,则△EFG的面积为