Question

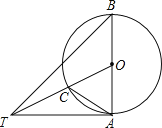
【题目】如图，AC是⊙O的直径，弦BD交AC于点E．

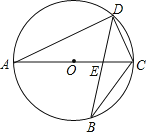
（1）求证：△ADE∽△BCE；

（2）如果AD2=AEAC，求证：CD=CB．

Answer 1

【答案】见解析

【解析】

试题分析：（1）由在同圆或等圆中，同弧或等弧所对的圆周角相等，即可得∠A=∠B，又由对顶角相等，可证得：△ADE∽△BCE；

（2）由AD2=AEAC，可得，又由∠A是公共角，可证得△ADE∽△ACD，又由AC是⊙O的直径，以求得AC⊥BD，由垂径定理即可证得CD=CB．

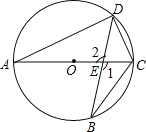
证明：（1）如图，∵∠A与∠B是对的圆周角，

∴∠A=∠B，

又∵∠1=∠2，

∴△ADE∽△BCE；

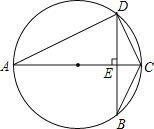
（2）如图，

∵AD2=AEAC，

∴，

又∵∠A=∠A，

∴△ADE∽△ACD，

∴∠AED=∠ADC，

又∵AC是⊙O的直径，

∴∠ADC=90°，

即∠AED=90°，

∴直径AC⊥BD，

∴=，

∴CD=CB．